早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,已知点A的坐标为(0,-1),点C(m,0)是x轴上的一个动点.(1)如图1,点B在第四象限,△AOB和△BCD都是等边三角形,点D在BC的上方,当点C在x轴上运动到如图所示
题目详情
在平面直角坐标系xOy中,已知点A的坐标为(0,-1),点C(m,0)是x轴上的一个动点.
(1)如图1,点B在第四象限,△AOB和△BCD都是等边三角形,点D在BC的上方,当点C在x轴上运动到如图所示的位置时,连接AD,请证明△ABD≌△OBC;
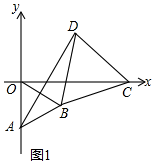
(2)如图2,点B在x轴的正半轴上,△ABO和△ACD都是等腰直角三角形,点D在AC的上方,∠D=90°,当点C在x轴上运动(m>1)时,设点D的坐标为(x,y),请探求y与x之间的函数表达式;
(3)如图3,四边形ACEF是菱形,且∠ACE=90°,点E在AC的上方,当点C在x轴上运动(m>1)时,设点E的坐标为(x,y),请探求y与x之间的函数表达式.
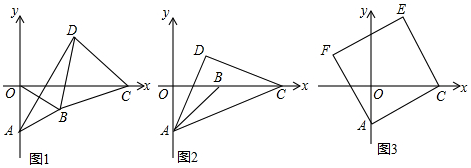
(1)如图1,点B在第四象限,△AOB和△BCD都是等边三角形,点D在BC的上方,当点C在x轴上运动到如图所示的位置时,连接AD,请证明△ABD≌△OBC;
(2)如图2,点B在x轴的正半轴上,△ABO和△ACD都是等腰直角三角形,点D在AC的上方,∠D=90°,当点C在x轴上运动(m>1)时,设点D的坐标为(x,y),请探求y与x之间的函数表达式;
(3)如图3,四边形ACEF是菱形,且∠ACE=90°,点E在AC的上方,当点C在x轴上运动(m>1)时,设点E的坐标为(x,y),请探求y与x之间的函数表达式.

▼优质解答
答案和解析
 (1)∵△AOB和△BCD都是等边三角形,
(1)∵△AOB和△BCD都是等边三角形,
∴AB=OB,BD=BC,∠ABO=∠DBC=60°,
∴∠ABD=∠OBC,
在△ABD和△OBC中,
,
∴△ABD和△OBC;
(2)如图,过点D作DH⊥y轴,垂足为H,延长HD,过点C作CG⊥HD,垂足为G.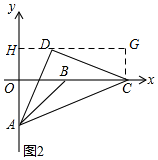
∴∠AHD=∠CGD=90°,
∵△ABO和△ACD都是等腰直角三角形,
∴∠ADC=90°,AD=CD,
∴∠ADH+∠CDG=90°,
∵∠ADH+∠DAH=90°,
∴∠CDG=∠DAH,
∵在△AHD和△DGC中,
,
∴△AHD≌△DGC(AAS),
∴DH=CG=OH,
∵点D的坐标为(x,y),
∴y与x之间的关系是y=x;
(3)过点E作EM⊥x轴,垂足为M,则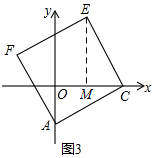 ∠EMC=∠COA=90°,
∠EMC=∠COA=90°,
∵四边形ACEF是菱形,且∠ACE=90°,
∴AC=CE,∠ACO+∠ECO=90°,
∵∠ACO+∠CAO=90°,
∴∠ECO=∠CAO,
在△EMC和△COA中,
,
∴△EMC≌△COA(AAS),
∴MC=OA=1,EM=OC,
∵点E的坐标为(x,y),
∴EM=OC=x+1,
∴y与x之间的关系是y=x+1.
 (1)∵△AOB和△BCD都是等边三角形,
(1)∵△AOB和△BCD都是等边三角形,∴AB=OB,BD=BC,∠ABO=∠DBC=60°,
∴∠ABD=∠OBC,
在△ABD和△OBC中,
|
∴△ABD和△OBC;
(2)如图,过点D作DH⊥y轴,垂足为H,延长HD,过点C作CG⊥HD,垂足为G.

∴∠AHD=∠CGD=90°,
∵△ABO和△ACD都是等腰直角三角形,
∴∠ADC=90°,AD=CD,
∴∠ADH+∠CDG=90°,
∵∠ADH+∠DAH=90°,
∴∠CDG=∠DAH,
∵在△AHD和△DGC中,
|
∴△AHD≌△DGC(AAS),
∴DH=CG=OH,
∵点D的坐标为(x,y),
∴y与x之间的关系是y=x;
(3)过点E作EM⊥x轴,垂足为M,则
 ∠EMC=∠COA=90°,
∠EMC=∠COA=90°,∵四边形ACEF是菱形,且∠ACE=90°,
∴AC=CE,∠ACO+∠ECO=90°,
∵∠ACO+∠CAO=90°,
∴∠ECO=∠CAO,
在△EMC和△COA中,
|
∴△EMC≌△COA(AAS),
∴MC=OA=1,EM=OC,
∵点E的坐标为(x,y),
∴EM=OC=x+1,
∴y与x之间的关系是y=x+1.
看了 在平面直角坐标系xOy中,已...的网友还看了以下:
已知:如图,在直角坐标系中,直角三角形OAB,O为坐标原点,AB=1,OB=3,将△OAB绕着A点 2020-05-13 …
已知椭圆x^2/2+y^2=1的左焦点为F,O为坐标原点,设过点F且不与坐标轴垂直的直线交椭已知椭 2020-05-16 …
在平面直角坐标系中,O为坐标原点,A,B,C三点满足向量OC = 2/3 向量OA + 1/3在平 2020-05-16 …
已知在矩形ABCD中,AB=4,BC=252,O为BC上一点,BO=72,如图所示,以BC所在直线 2020-06-12 …
如图,在矩形ABCD中,AB=4,BC=25/2,O为BC上一点,BO=7/2如图所示,以BC所在 2020-06-12 …
已知在矩形ABCD中,AB=4,BC=252,O为BC上一点,BO=72,如图所示,以BC所在直线 2020-07-19 …
数学题在平面直角坐标系中,O为坐标原点,已知向量a=(1,2),点A(1,0),B(cosX,T) 2020-08-01 …
在平面直角坐标系中,O为坐标原点,点A的坐标为(2x+y-3,x-2y),它关于x轴的对称点A1的 2020-08-01 …
已知以点C(t,2/t)),(t>0)为圆心的圆与与X轴交与O,A,与Y轴交与点O,B其中O为坐标 2020-08-02 …
在空间直角坐标系O-xyz中O为坐标原点,点A,B在空间直角坐标系O-xyz中O为坐标原点,点A, 2020-08-02 …