早教吧作业答案频道 -->数学-->
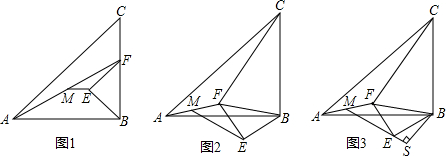
如图1,等腰直角△ABC和等腰直角△BEF,∠ABC=∠BEF=90°,点F在边BC上,点M为AF的中点,连EM.(1)①在图1中画出△BEF关于直线BE成轴对称的三角形;②求证:CF=2ME;(2)将图1中的△BEF绕点B
题目详情
如图1,等腰直角△ABC和等腰直角△BEF,∠ABC=∠BEF=90°,点F在边BC上,点M为AF的中点,连EM.
(1)①在图1中画出△BEF关于直线BE成轴对称的三角形;
②求证:CF=2ME;
(2)将图1中的△BEF绕点B逆时针旋转至如图2的位置,其他条件不变,(1)中的结论②是否仍成立?请证明你的结论;
(3)如图3,过B作BS⊥ME于S,若ES=2,BS=4,CF=10,则S四边形CFEB为___(直接写出结果)
(1)①在图1中画出△BEF关于直线BE成轴对称的三角形;
②求证:CF=2ME;
(2)将图1中的△BEF绕点B逆时针旋转至如图2的位置,其他条件不变,(1)中的结论②是否仍成立?请证明你的结论;
(3)如图3,过B作BS⊥ME于S,若ES=2,BS=4,CF=10,则S四边形CFEB为___(直接写出结果)

▼优质解答
答案和解析
(1) ①延长EF交AB于D,如图1,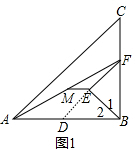
∵等腰直角△ABC和等腰直角△BEF,∠ABC=∠BEF=90°,
∴∠1=∠BFE=45°,
∴∠2=∠BDE=45°,
∴EF=ED=BE,
即BE垂直平分DF,
∴△BED与△BEF关于直线BE对称,
即△BED为所作;
②证明∵M点为AF的中点,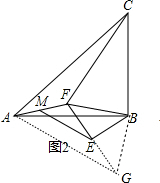
而EF=ED,
∴ME为△FAD的中位线,
∴AD=2ME,
∵BD=BF,BA=BC,
∴AD=CF,
∴CF=2ME;
(2) (1)中的结论②仍成立.理由如下:
延长FE到点G,使EG=EF,如图2,连结AG、BG,
∵M点为AF的中点,
而EF=EG,
∴ME为△FAG的中位线,
∴AG=2ME,
∵△BEF为等腰直角三角形,
∴∠BEF=90°,BE=EF,
而EF=EG,
∴△BEG为等腰直角三角形,
∴∠BGE=∠EBG=45°,
∴△FBG为等腰直角三角形,
∴BF=BG,∠FBG=90°,
∵∠ABG+∠ABF=90°,∠CBF+∠ABF=90°,
∴∠ABG=∠CBF,
在△ABG和△CBF中
,
∴△ABG≌△CBF,
∴AG=CF,
∴CF=2ME;
(4)延长FE到点G,使EG=EF,如图3,连结AG、BG,作FH⊥ME于H,交AG于L,延长BS交AG于K,
由(3)得△ABG≌△CBF,
∴AG=CF=10,S△ABG=S△CBF,
∵∠FEH+∠BES=90°,∠EBS+∠BES=90°,
∴∠FEH=∠EBS,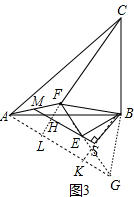
在△FEH和△EBS中
,
∴△FEH≌△EBS,
∴FH=ES=2,
∵ME为△FAG的中位线,
∴FH=HL=2,ME∥AG,
易得四边形HLKS为矩形,
∴SK=HL=2,
∴BK=BS+SK=4+2=6,
∴S△ABG=
•10•6=30,
∴S△CBF=30,
在Rt△BES中,BE=
=2
,
∴S△BEF=
•2
•2
=10,
∴S四边形CFEB=S△BCF+S△BEF=30+10=40.
故答案为40.

∵等腰直角△ABC和等腰直角△BEF,∠ABC=∠BEF=90°,
∴∠1=∠BFE=45°,
∴∠2=∠BDE=45°,
∴EF=ED=BE,
即BE垂直平分DF,
∴△BED与△BEF关于直线BE对称,
即△BED为所作;
②证明∵M点为AF的中点,

而EF=ED,
∴ME为△FAD的中位线,
∴AD=2ME,
∵BD=BF,BA=BC,
∴AD=CF,
∴CF=2ME;
(2) (1)中的结论②仍成立.理由如下:
延长FE到点G,使EG=EF,如图2,连结AG、BG,
∵M点为AF的中点,

而EF=EG,
∴ME为△FAG的中位线,
∴AG=2ME,
∵△BEF为等腰直角三角形,
∴∠BEF=90°,BE=EF,
而EF=EG,
∴△BEG为等腰直角三角形,
∴∠BGE=∠EBG=45°,
∴△FBG为等腰直角三角形,
∴BF=BG,∠FBG=90°,
∵∠ABG+∠ABF=90°,∠CBF+∠ABF=90°,
∴∠ABG=∠CBF,
在△ABG和△CBF中
|
∴△ABG≌△CBF,
∴AG=CF,
∴CF=2ME;
(4)延长FE到点G,使EG=EF,如图3,连结AG、BG,作FH⊥ME于H,交AG于L,延长BS交AG于K,
由(3)得△ABG≌△CBF,
∴AG=CF=10,S△ABG=S△CBF,
∵∠FEH+∠BES=90°,∠EBS+∠BES=90°,
∴∠FEH=∠EBS,

在△FEH和△EBS中
|
∴△FEH≌△EBS,
∴FH=ES=2,
∵ME为△FAG的中位线,
∴FH=HL=2,ME∥AG,
易得四边形HLKS为矩形,
∴SK=HL=2,
∴BK=BS+SK=4+2=6,
∴S△ABG=
| 1 |
| 2 |
∴S△CBF=30,
在Rt△BES中,BE=
| 22+42 |
| 5 |
∴S△BEF=
| 1 |
| 2 |
| 5 |
| 5 |
∴S四边形CFEB=S△BCF+S△BEF=30+10=40.
故答案为40.
看了 如图1,等腰直角△ABC和等...的网友还看了以下:
在一定温度下,化学平衡常数K=(C)c(D)d / (A)a(B)b.给定AB的浓度 达到平衡 就 2020-04-06 …
(1)x/a+x/b-a+a/a+b(a不等于0,axa不等于bxb)(2)(mx-n)(m+n) 2020-04-07 …
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
1.已知a+b=0,且a不是0,则当n是自然数时,下列式子正确的是:A.a^2n+b^2n=0Ba 2020-05-13 …
设P(A)=a,P(B)=b.如果AB不相容,求P(AUB)=如果AB相互独立.求P(AUB)=如 2020-06-12 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
写出集合A={a,b,c}的所有子集和真子集拜托各位大神子集:空集,{a},{b},{c},{a, 2020-07-29 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …