早教吧作业答案频道 -->数学-->
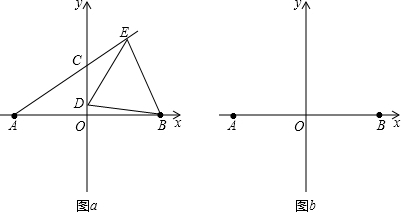
在平面直角坐标系xOy中,点A(a,0),点B(b,0)是x轴上两点,其中a2+2ab+b2+|b-4|=0,点C,D都在y轴上,E在射线AC上(不与点A重合),DB=DE,连结BE.(1)求A、B的坐标;(2)如图a,若C在y轴
题目详情
在平面直角坐标系xOy中,点A(a,0),点B(b,0)是x轴上两点,其中a2+2ab+b2+|b-4|=0,点C,D都在y轴上,E在射线AC上(不与点A重合),DB=DE,连结BE.
(1)求A、B的坐标;
(2)如图a,若C在y轴正半轴,D在线段OC上,当∠CAO=30°时,求证:△BDE为等边三角形;(提示:连结AD…)
(3)当BD⊥DE时,在图b中画出示意图,设E(m,n),若mn=2,求
+
的值.
(1)求A、B的坐标;
(2)如图a,若C在y轴正半轴,D在线段OC上,当∠CAO=30°时,求证:△BDE为等边三角形;(提示:连结AD…)
(3)当BD⊥DE时,在图b中画出示意图,设E(m,n),若mn=2,求
| n |
| m |
| m |
| n |

▼优质解答
答案和解析
(1)∵a2+2ab+b2+|b-4|=0,
∴(a+b)2+|b-4|=0,
又∵(a+b)2≥0,|b-4|≥0,
∴(a+b)2=0,|b-4|=0,
∴a=-4,b=4,
∴A(-4,0),B(4,0);
(2)证明:如图a,连接AD并延长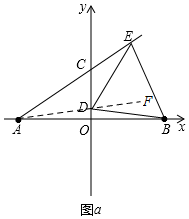 至F,
至F,
∵A(-4,0),B(4,0),
∴OA=OB,
∵OD⊥AB,
∴DA=DB,
∴∠DAO=∠DBO,
∴∠BDF=∠DAO+∠DBO=2∠DAO,
∵DA=DB,DE=DB,
∴DA=DE,
同理可得∠EDF=2∠DAE,
∴∠BDF+∠EDF=2∠DAE+2∠DAO=2∠CAO=60°,
即∠EDB=60°,
又∵DE=DB,
∴△BDE为等边三角形;
(3)分两种情况: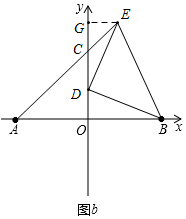
①当C在y轴正半轴时,如图b所示,过点E作EG⊥y轴于点G,则∠GED+∠GDE=90°,
∵DE⊥DB,
∴∠ODB+∠GDE=90°,
∴∠GED=∠ODB,
又∵∠DGE=∠DOB=90°,DE=DB,
∴在△DGE和△BOD中,
,
∴△DGE≌△BOD(AAS)
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=m,OG=n,
由OG-OD=DG,得n-m=4,
∵mn=2,
∴
+
=
=
=
=10;
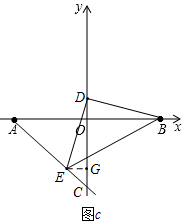
②当C在y轴负半轴时,如图c所示,过点E作EG⊥y轴于点G,
同理可得,△DGE≌△BOD,
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=-m,OG=-n,
由OD+OG=DG,得-m+(-n)=4,则m+n=-4,
∵mn=2,
∴
+
=
=
=
=6,
综上所述,
+
的值为10或6.
∴(a+b)2+|b-4|=0,
又∵(a+b)2≥0,|b-4|≥0,
∴(a+b)2=0,|b-4|=0,
∴a=-4,b=4,
∴A(-4,0),B(4,0);
(2)证明:如图a,连接AD并延长
 至F,
至F,∵A(-4,0),B(4,0),
∴OA=OB,
∵OD⊥AB,
∴DA=DB,
∴∠DAO=∠DBO,
∴∠BDF=∠DAO+∠DBO=2∠DAO,
∵DA=DB,DE=DB,
∴DA=DE,
同理可得∠EDF=2∠DAE,
∴∠BDF+∠EDF=2∠DAE+2∠DAO=2∠CAO=60°,
即∠EDB=60°,
又∵DE=DB,
∴△BDE为等边三角形;
(3)分两种情况:

①当C在y轴正半轴时,如图b所示,过点E作EG⊥y轴于点G,则∠GED+∠GDE=90°,
∵DE⊥DB,
∴∠ODB+∠GDE=90°,
∴∠GED=∠ODB,
又∵∠DGE=∠DOB=90°,DE=DB,
∴在△DGE和△BOD中,
|
∴△DGE≌△BOD(AAS)
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=m,OG=n,
由OG-OD=DG,得n-m=4,
∵mn=2,
∴
| n |
| m |
| m |
| n |
| m2+n2 |
| mn |
| (n-m)2+2mn |
| mn |
| 42+2×2 |
| 2 |

②当C在y轴负半轴时,如图c所示,过点E作EG⊥y轴于点G,
同理可得,△DGE≌△BOD,
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=-m,OG=-n,
由OD+OG=DG,得-m+(-n)=4,则m+n=-4,
∵mn=2,
∴
| n |
| m |
| m |
| n |
| m2+n2 |
| mn |
| (m+n)2-2mn |
| mn |
| (-4)2-2×2 |
| 2 |
综上所述,
| n |
| m |
| m |
| n |
看了 在平面直角坐标系xOy中,点...的网友还看了以下:
如图,已知点F(1,0),点A,B分别在x轴、y轴上运动,且满足AB⊥BF,AD=2AB,设点D的 2020-06-12 …
在平面直角坐标系xOy中,点A(a,0),点B(b,0)是x轴上两点,其中a2+2ab+b2+|b 2020-07-19 …
(2014•邯郸二模)如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC 2020-07-20 …
(2014•温州五校一模)如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0) 2020-07-21 …
已知A、B是数轴上两点,A点对应数为12,B点对应数为42.(1)C是数轴上一点,且AC=2AB, 2020-07-21 …
(2012•武汉)如图,点A在双曲线y=kx的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴 2020-07-24 …
如图,点A在反比例函数y=kx(x>0)的图象上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2 2020-07-24 …
如图,点A在双曲线y=kx的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC= 2020-07-26 …
如图,点A(0,a),B(b,0)分别在y轴正半轴、x轴正半轴上,C为AB的中点,a,b满足a2- 2020-07-30 …
已知椭圆上的点到左右两焦点的距离之和为,离心率为.(1)求椭圆的方程;(2)过右焦点的直线交椭圆于 2020-07-31 …