早教吧作业答案频道 -->数学-->
已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.(1)如图1,连接AF,若AB=4,BE=1,求AF的长;(2)如图2,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求
题目详情
已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.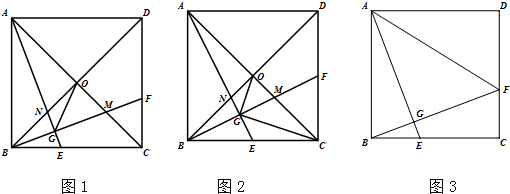
(1)如图1,连接AF,若AB=4,BE=1,求AF的长;
(2)如图2,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求证:GO平分∠AGF;
(3)如图3,在第(2)问的条件下,连接CG,若CG⊥GO,求证:AG=
CG.

(1)如图1,连接AF,若AB=4,BE=1,求AF的长;
(2)如图2,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求证:GO平分∠AGF;
(3)如图3,在第(2)问的条件下,连接CG,若CG⊥GO,求证:AG=
| 2 |
▼优质解答
答案和解析
(1) ∵四边形ABCD是正方形,
∴BC=CD=AD=AB=4,∠ABE=∠C=∠D=90°,AC⊥BD,∠ABO=45°,
∴∠ABG+∠CBF=90°,
∵BF⊥AE,
∴∠ABG+∠BAE=90°,
∴∠BAE=∠CBF,
在△BCF和△ABE中,
,
∴△BCF≌△ABE(ASA),
∴CF=BE=1,
∴DF=CD=CF=3,
∴AF=
=5;
(2)证明:∵AC⊥BD,BF⊥AE,
∴∠AOB=∠AGB=∠AGF=90°,
∴A、B、G、O四点共圆,
∴∠AGO=∠ABO=45°,
∴∠FGO=90°-45°=45°=∠AGO,
∴GO平分∠AGF;
(3)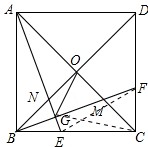 证明:连接EF,如图所示:
证明:连接EF,如图所示:
∵CG⊥GO,
∴∠OGC=90°,
∵∠EGF=∠BCD=90°,
∴∠EGF+∠BCD=180°,
∴C、E、G、F四点共圆,
∴∠EFC=∠EGC=180°-90°-45°=45°,
∴△CEF是等腰直角三角形,
∴CE=CF,
同(1)得:△BCF≌△ABE,
∴CF=BE,
∴CE=BE=
BC,
∴OA=
AC=
BC=
CE,
由(1)得:A、B、G、O四点共圆,
∴∠BOG=∠BAE,
∵∠GEC=90°+∠BAE,∠GOA=90°+∠BOG,
∴∠GOA=∠GEC,
又∵∠EGC=∠AGO=45°,
∴△AOG∽△CEG,
∴
=
=
,
∴AG=
CG.
∴BC=CD=AD=AB=4,∠ABE=∠C=∠D=90°,AC⊥BD,∠ABO=45°,
∴∠ABG+∠CBF=90°,
∵BF⊥AE,
∴∠ABG+∠BAE=90°,
∴∠BAE=∠CBF,
在△BCF和△ABE中,
|
∴△BCF≌△ABE(ASA),
∴CF=BE=1,
∴DF=CD=CF=3,
∴AF=
| 42+32 |
(2)证明:∵AC⊥BD,BF⊥AE,
∴∠AOB=∠AGB=∠AGF=90°,
∴A、B、G、O四点共圆,
∴∠AGO=∠ABO=45°,
∴∠FGO=90°-45°=45°=∠AGO,
∴GO平分∠AGF;
(3)
 证明:连接EF,如图所示:
证明:连接EF,如图所示:∵CG⊥GO,
∴∠OGC=90°,
∵∠EGF=∠BCD=90°,
∴∠EGF+∠BCD=180°,
∴C、E、G、F四点共圆,
∴∠EFC=∠EGC=180°-90°-45°=45°,
∴△CEF是等腰直角三角形,
∴CE=CF,
同(1)得:△BCF≌△ABE,
∴CF=BE,
∴CE=BE=
| 1 |
| 2 |
∴OA=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
由(1)得:A、B、G、O四点共圆,
∴∠BOG=∠BAE,
∵∠GEC=90°+∠BAE,∠GOA=90°+∠BOG,
∴∠GOA=∠GEC,
又∵∠EGC=∠AGO=45°,
∴△AOG∽△CEG,
∴
| AG |
| CG |
| OA |
| CE |
| 2 |
∴AG=
| 2 |
看了 已知正方形ABCD中,点E在...的网友还看了以下:
把函数y=e^x的图像按向量a=(2,3)平移,得到y=f(x)的图像,则f(x)=?A.e^(x 2020-05-16 …
已知b分之a=d分之c=f分之e=2且b+d+f≠0.(1)b+d+f分之a+c+e=(2)b-d 2020-06-09 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
数学分析习题.设函数f(x)在[a,b]上三阶可导,证明:存在一点e∈(a,b)设函数f(x)在[ 2020-07-16 …
一带负点金属球,体积大小不能忽略,其附近某点的电场强度为E.若在该点放一带正点的点电荷q,且测得q 2020-07-20 …
已知直角坐标系平面内点A(4,0)B(2,-2),C(1,1)在直角坐标平面内求一点P,使点A,B 2020-07-31 …
设函数f(x)在[a,b]上三阶可导,证明:存在一点e∈(a,b),使得f(b)=f(a)+1/2 2020-08-02 …
````某大学宿舍里有A.B.C.D.E.F.G.七位同学.其中两位来自哈尔滨,两位来自天津.两位来 2020-11-12 …
数学广角判真假题某大学宿舍里有A.B.C.D.E.F.G.七位同学.其中两位来字哈尔滨,两位来自天津 2020-11-12 …
代数化简法化简1.L=A*B*非C+非(A*B*C)*非(A*B)1.L=A*B*非C+非(A*B* 2020-12-07 …