早教吧作业答案频道 -->数学-->
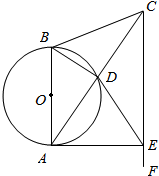
如图,在△ABC中,AB=CB,以AB为直径的O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=DC;②△CBA∽△CDE;③BD=
题目详情
如图,在△ABC中,AB=CB,以AB为直径的 O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=DC;②△CBA∽△CDE;③
=
;④AE为 O的切线,一定正确的结论选项是___.
 |
| BD |
 |
| AD |

▼优质解答
答案和解析
∵AB为直径,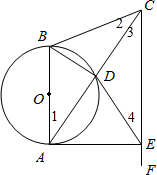
∴∠ADB=90°,
∴BD⊥AC,
而AB=CB,
∴AD=DC,所以①正确;
∵AB=CB,
∴∠1=∠2,
而CD=ED,
∴∠3=∠4,
∵CF∥AB,
∴∠1=∠3,
∴∠1=∠2=∠3=∠4,
∴△CBA∽△CDE,所以②正确;
∵△ABC不能确定为直角三角形,
∴∠1不能确定等于45°,
∴
和
不能确定相等,所以③错误;
∵DA=DC=DE,
∴点E在以AC为直径的圆上,
∴∠AEC=90°,
∴CE⊥AE,
而CF∥AB,
∴AB⊥AE,
∴AE为 O的切线,所以④正确.
故答案为①②④.

∴∠ADB=90°,
∴BD⊥AC,
而AB=CB,
∴AD=DC,所以①正确;
∵AB=CB,
∴∠1=∠2,
而CD=ED,
∴∠3=∠4,
∵CF∥AB,
∴∠1=∠3,
∴∠1=∠2=∠3=∠4,
∴△CBA∽△CDE,所以②正确;
∵△ABC不能确定为直角三角形,
∴∠1不能确定等于45°,
∴
 |
| BD |
 |
| AD |
∵DA=DC=DE,
∴点E在以AC为直径的圆上,
∴∠AEC=90°,
∴CE⊥AE,
而CF∥AB,
∴AB⊥AE,
∴AE为 O的切线,所以④正确.
故答案为①②④.
看了 如图,在△ABC中,AB=C...的网友还看了以下:
连字成词(英语)l u o e b s r u s r e t o s w a e s r t e 2020-05-14 …
如图所示,平行四边形ABCD的对角线AC的垂直平分线EF与AD,BC,AC分别交于点E,F,O,连 2020-05-15 …
如图,AB为⊙O的直径,C为⊙O上一点,作CD⊥AB,垂足为D,E为弧BC的中点,连接AE、BE, 2020-05-16 …
已知e为平行四边形abcd中dc边延长线上一点,且ce=dc,连ae分别交bc bd于f g,连已 2020-05-16 …
如图,直线y=-根号3/3x+根号3分别与x轴y轴交于点A.B,⊙E经过原点O及A.B两点,⊙E经 2020-06-14 …
如图,在Rt三角形ABC中,角C=90度,AE平分角BAC交BC于E,点O在AB上,以OA为半径的 2020-06-27 …
如图,AB是O的直径,D、E为O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接A 2020-07-17 …
(2014•通州区一模)如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与C 2020-07-20 …
如图所示,要测水池中一荷花E距岸边A和岸边D的距离.作法如下:(1)任作线段AB,取其中点O;(2) 2020-11-01 …
在平面直角坐标系中,已知A(-1.0)B(0.2)点C在第二象限,CD⊥x轴,垂足为D,且△CDA≌ 2021-01-22 …