高为1的四棱锥S-ABCD的底面是边长为2的正方形，点S、A、B、C、D均在半径为172的同一球面上，在底面ABCD的中心与顶点S之间的距离为（）A.22B.52C.5D.2

Question

高为1的四棱锥S-ABCD的底面是边长为2的正方形，点S、A、B、C、D均在半径为

(√(17))/(2)的同一球面上，在底面ABCD的中心与顶点S之间的距离为（　　）

A.

(√(2))/(2)

B.

(√(5))/(2)

C.

√(5)

D.

√(2)

Answer 1

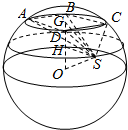由题意，设正方形ABCD的中心为G，可得
∵ABCD所在的圆是小圆，对角线长为2√(2)，即小圆半径为r=√(2)
∵点S、A、B、C、D均在半径为(√(17))/(2)的同一球面上，
∴球心到小圆圆心的距离OG=(3)/(2)，
∵四棱锥S-ABCD的高为1，
∴点S与ABCD所在平面的距离等于1，
设平面α∥平面ABCD，且它们的距离等于1，平面α截球得小圆的圆心为H，
则OH=(1)/(2)，
∴Rt△SOH中，SH²=OS²-OH²=R²-（(1)/(2)）²=4，
可得SG√(4+1)=√(5)，即底面ABCD的中心G与顶点S之间的距离为√(5)
故选：C．