早教吧作业答案频道 -->数学-->
O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.(1)如图(1),若∠AOB=130°,求∠EOF的度数;(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;(3)若∠AOB=α,0°<α<90°,请在图(2)中
题目详情
O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.
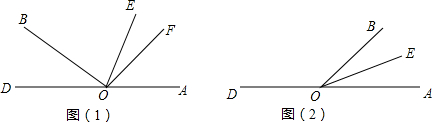
(1)如图(1),若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;
(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.
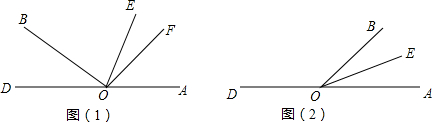
(1)如图(1),若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;
(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.
▼优质解答
答案和解析
(1)∵∠AOB=130°,EO是∠AOB的平分线,
∴∠AOE=
∠AOB=
×130°=65°,
∵OB⊥OF,
∴∠BOF=90°,
∴∠AOF=∠AOB-∠BOF=130°-90°=40°,
∴∠EOF=∠AOE-∠AOF=65°-40°=25°;
(2)∵∠AOB=α,90°<α<180°,EO是∠AOB的平分线,
∴∠AOE=
α,
∵∠BOF=90°,
∴∠AOF=α-90°,
∴∠EOF=∠AOE-∠AOF=
α-(α-90°)=90°-
α;
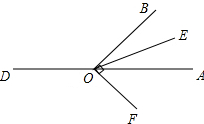
(3)如图,∵∠AOB=α,0°<α<90°,
∴∠BOE=∠AOE=
α,
∵∠BOF=90°,
∴∠EOF=∠BOF-∠BOE=90°-
α.
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵OB⊥OF,
∴∠BOF=90°,
∴∠AOF=∠AOB-∠BOF=130°-90°=40°,
∴∠EOF=∠AOE-∠AOF=65°-40°=25°;
(2)∵∠AOB=α,90°<α<180°,EO是∠AOB的平分线,
∴∠AOE=
| 1 |
| 2 |
∵∠BOF=90°,
∴∠AOF=α-90°,
∴∠EOF=∠AOE-∠AOF=
| 1 |
| 2 |
| 1 |
| 2 |

(3)如图,∵∠AOB=α,0°<α<90°,
∴∠BOE=∠AOE=
| 1 |
| 2 |
∵∠BOF=90°,
∴∠EOF=∠BOF-∠BOE=90°-
| 1 |
| 2 |
看了 O为直线DA上一点,OB⊥O...的网友还看了以下:
设f(x,y)在(0,0)处连续,limx,y→0f(x,y)-1ex2+y2-1=4,则()A. 2020-05-14 …
快,急.已知坐标系平面内的三个点A(1,3)B(3,1)O(0,0),求出三角形ABO的面积.快, 2020-05-16 …
给出平面上4个点O(0,0),A(3,0),B(0,3),C(sina,cosa),(1)若向量A 2020-05-16 …
有个excel函数问题想请教、当B1>0时候判定A1是否大于0若大于0则H1等于0若小于0则等于1 2020-07-30 …
已知xyz三维坐标系上点A(0,0,1),B(1,1,0),C(0,1,0),O(0,0,0),已 2020-07-30 …
已知在直角坐标系xOy中,直线l的参数方程为x=1+tcosαy=tsinα(t为参数,0<α<π 2020-07-31 …
如图1,已知四边形OABC中的三个顶点坐标为O(0,0),A(0,n),C(m,0).动点P从点O出 2020-10-31 …
若ab=0,则a=0或b=0,若ab=0,则a‖b,若a‖b,则a在b上的投影为丨a丨,若a⊥b,则 2020-11-02 …
使用mathematica求解多元不等式整数解出错,tt={10.11,14.31,17.48,25 2020-12-14 …
△=0,△<0时一元二次方程ax2+bx+c=0(a>0)的根根需要用字母代表出来△>0,△=0,△ 2020-12-27 …