早教吧作业答案频道 -->数学-->
如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.(1)求证:DE是⊙O的切线;(2)若AE:EB=1:2,BC=6,求AE的长.
题目详情
如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
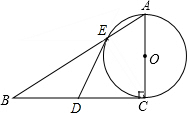
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求AE的长.

(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求AE的长.
▼优质解答
答案和解析
(1)证明: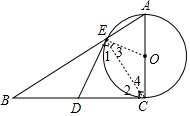
连接OE、EC,
∵AC是⊙O的直径,
∴∠AEC=∠BEC=90°,
∵D为BC的中点,
∴ED=DC=BD,
∴∠1=∠2,
∵OE=OC,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠OED=∠ACB,
∵∠ACB=90°,
∴∠OED=90°,
∴DE是⊙O的切线;
(2) 由(1)知:∠BEC=90°,
∵在Rt△BEC与Rt△BCA中,∠B=∠B,∠BEC=∠BCA,
∴△BEC∽△BCA,
∴
=
,
∴BC2=BE•BA,
∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x,
∵BC=6,
∴62=2x•3x,
解得:x=
,
即AE=
.

连接OE、EC,
∵AC是⊙O的直径,
∴∠AEC=∠BEC=90°,
∵D为BC的中点,
∴ED=DC=BD,
∴∠1=∠2,
∵OE=OC,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠OED=∠ACB,
∵∠ACB=90°,
∴∠OED=90°,
∴DE是⊙O的切线;
(2) 由(1)知:∠BEC=90°,
∵在Rt△BEC与Rt△BCA中,∠B=∠B,∠BEC=∠BCA,
∴△BEC∽△BCA,
∴
| BE |
| BC |
| BC |
| BA |
∴BC2=BE•BA,
∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x,
∵BC=6,
∴62=2x•3x,
解得:x=
| 6 |
即AE=
| 6 |
看了 如图,已知Rt△ABC,∠C...的网友还看了以下:
已知曲线C的方程为y2=4x(x>0),曲线E是以F1(-1,0)、F2(1,0)为焦点的椭圆,点 2020-05-15 …
(2014•洛阳二模)已知椭圆E:x2a2+y2b2=1(a>b>0)的左右焦点分别是F1,F2, 2020-05-15 …
椭圆E中心在坐标原点,焦点在x轴上,其离心率e=√ 6/3,过点C(-1,0)的直线l与椭圆E相交 2020-05-16 …
已知F是双曲线E:x2a2-y2b2=1(a>0,b>0)的右焦点,过点F作E的一条渐近线的垂线, 2020-07-09 …
如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是()A.∠1和∠2B 2020-07-23 …
已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足PM=MP′,当P在圆上运动 2020-07-30 …
动圆G与圆Q1:X2+Y2+2X=0外切,同时与圆O2:X2+Y2-2X-8=0内切,设动圆圆心G 2020-07-31 …
已知椭圆E:X2/a2+Y2/b2=1(a>b>0)过点P(1,√2/2),离心率e=√2/2.椭 2020-08-01 …
如图,已知三角形ABC内接于圆O,AD平分角BAC,交于圆O于D,交于BC于E,连结BD、CD,求 2020-08-03 …
已知椭圆E:x^2/a^2+y^2/b^2=1(a>b>0)的右焦点为F(c,0),(c>b).过原 2021-01-11 …