在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0<α≤180°），记直线BD1与CE1的交点为P．

Question

在Rt△ ABC中，∠ A=90°，AC=AB=4， D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD ₁ E ₁ ，设旋转角为 α （0< α ≤180°），记直线BD ₁ 与CE ₁ 的交点为P．

（1）如图1，当 α =90°时，线段BD ₁ 的长等于         ，线段CE ₁ 的长等于         ；（直接填写结果）

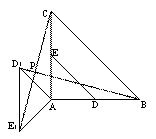
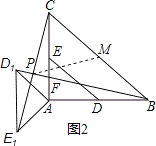
（2）如图2，当 α =135°时，求证：BD ₁ = CE ₁ ，且BD ₁ ⊥CE ₁ ；

（3）①设BC的中点为M，则线段PM的长为         ；②点P到AB所在直线的距离的最大值为         ．（直接填写结果）

 

Answer 1

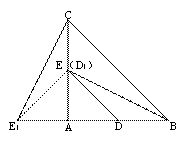
（1） ∵∠ A=90° ，AC=AB=4，D，E分别是边AB，AC的中点，

∴ AE=AD=2 ，

∵ 等腰Rt △ ADE 绕点A逆时针旋转，得到等腰Rt △ AD ₁ E ₁ ，设旋转角为α（0＜α≤180°），

∴ 当α=90°时，AE ₁ =2， ∠ E ₁ AE=90°，

∴ BD ₁ = =2 ，E ₁ C= =2 ；

故答案为：2 ，2 ；

（2）证明：当α=135°时，如图2，

∵ Rt △ AD ₁ E是由Rt △ ADE 绕点A逆时针旋转135°得到，

∴ AD ₁ =AE ₁ ， ∠ D ₁ AB= ∠ E ₁ AC=135°，

在 △ D ₁ AB和 △ E ₁ AC中

∵ ，

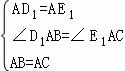∴△ D ₁ AB ≌△ E ₁ AC（SAS），

∴ BD ₁ =CE ₁ ，且 ∠ D ₁ BA= ∠ E ₁ CA，

记直线BD ₁ 与AC交于点F，

∴∠ BFA= ∠ CFP ，

∴∠ CPF= ∠ FAB=90° ，

∴ BD ₁ ⊥ CE ₁ ；

（3） ①∵∠ CPB= ∠ CAB=90° ，BC的中点为M，

∴ PM= BC，

∴ PM= =2 ，

故答案为：2 ；

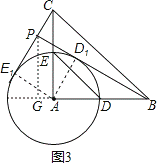
② 如图3，作PG ⊥ AB，交AB所在直线于点G，

∵ D ₁ ，E ₁ 在以A为圆心，AD为半径的圆上，

当BD ₁ 所在直线与 ⊙ A 相切时，直线BD ₁ 与CE ₁ 的交点P到直线AB的距离最大，

此时四边形AD ₁ PE ₁ 是正方形，PD ₁ =2，则BD ₁ = =2 ，

故 ∠ ABP=30° ，

则PB=2+2 ，

故点P到AB所在直线的距离的最大值为：PG=1+ ．

故答案为：1+ ．