早教吧作业答案频道 -->数学-->
已知:在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.(1)如图1,若AE、CD为△ABC的角平分线.①求证:∠AFC=120°;②若AD=6,CE=4,求AC的长?(2)如图2,若∠FAC=∠FCA=30°,
题目详情
已知:在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线.
①求证:∠AFC=120°;
②若AD=6,CE=4,求AC的长?
(2)如图2,若∠FAC=∠FCA=30°,求证:AD=CE.
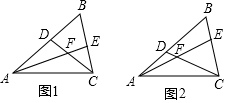
(1)如图1,若AE、CD为△ABC的角平分线.
①求证:∠AFC=120°;
②若AD=6,CE=4,求AC的长?
(2)如图2,若∠FAC=∠FCA=30°,求证:AD=CE.

▼优质解答
答案和解析
(1)①∵AE、CD分别为△ABC的角平分线
∴∠FAC=
∠BAC,∠FCA=
∠BCA,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180-∠FAC-∠FCA=180-
(∠BAC+∠BCA)=120°.
②在AC上截取AG=AD=6,连接FG.
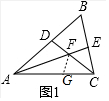
∵AE、CD分别为△ABC的角平分线
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中
,
∴△ADF≌△AGF(SAS)
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中
,
∴△CGF≌△CEF(ASA),
∴CG=CE=4,
∴AC=10.
(2)在AE上截取FH=FD,连接CH.
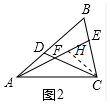
∵∠FAC=∠FCA=30°
∴FA=FC,
在△ADF和△CHF中
∵
,
∴△ADF≌△CHF(SAS),
∴AD=CH,∠DAF=∠HCF,
∵∠CEH=∠B+∠DAF=60°+∠DAF
∠CHE=∠HAC+∠HCA=60°+∠HCF
∴∠CEH=∠CHE,
∴CH=CE,
∴AD=CE.
∴∠FAC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180-∠FAC-∠FCA=180-
| 1 |
| 2 |
②在AC上截取AG=AD=6,连接FG.

∵AE、CD分别为△ABC的角平分线
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中
|
∴△ADF≌△AGF(SAS)
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中
|
∴△CGF≌△CEF(ASA),
∴CG=CE=4,
∴AC=10.
(2)在AE上截取FH=FD,连接CH.

∵∠FAC=∠FCA=30°
∴FA=FC,
在△ADF和△CHF中
∵
|
∴△ADF≌△CHF(SAS),
∴AD=CH,∠DAF=∠HCF,
∵∠CEH=∠B+∠DAF=60°+∠DAF
∠CHE=∠HAC+∠HCA=60°+∠HCF
∴∠CEH=∠CHE,
∴CH=CE,
∴AD=CE.
看了 已知:在△ABC中,∠B=6...的网友还看了以下:
下列条件中,能判定△ABC∽△A′B′C′的是()A.∠A=50°,∠B=40°,∠A′=40°, 2020-05-13 …
弱酸HA的电离常数K=c(H+)•c(A-)c(HA).25℃时,有关弱酸的电离常数如下:弱酸化学 2020-05-14 …
某无息债券的面值为1000元,期限为2年,发行价为880元,到期按面值偿还该债券的复利到期收益率为 2020-06-07 …
有4个数字A、B、C、D它们的和不超过400,并且A÷B=5余5,A÷C=6余6,A÷D=7余7, 2020-06-14 …
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线 2020-06-27 …
△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2B2.(1)求co 2020-07-09 …
在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列关系式中错误的是()A 2020-07-15 …
在三角形ABC中,内角A,B,C所对的边分别为a,b,c已知a-c=6分之根号6b,sinB=根号 2020-07-19 …
设a=log36,b=log510,c=log714,则().A.c>b>aB.b>c>aC.a> 2020-07-21 …
已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c.若a=c=6+2,且∠A=75°,则b=( 2020-08-02 …