早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=26.(1)求证:A′C⊥EF;(2)求五棱锥A′-BCDFE的体积.
题目详情
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
.
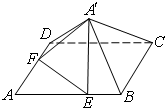
(1)求证:A′C⊥EF;
(2)求五棱锥A′-BCDFE的体积.
| 6 |

(1)求证:A′C⊥EF;
(2)求五棱锥A′-BCDFE的体积.
▼优质解答
答案和解析
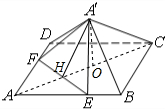 (1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,
(1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,
∵AC∩A′H=H,
∴EF⊥平面A′HC,
∵A′C⊂平面A′HC,
∴A′C⊥EF;
(2) 由ABCD是正方形,AE=AF=4,
得H是EF的中点,
且EF⊥AH,EF⊥CH,
从而有A′H⊥EF,CH⊥EF,
∴EF⊥平面A′HC,
从而平面A′HC⊥平面ABCD,
过点A′作A′O垂直HC且与HC相交于点O,
则A′O⊥平面ABCD.
∵正方形ABCD的边长为6,AE=AF=4,
得到:A′H=2
,CH=4
,
∴cos∠A′HC=
=
,
∴HO=A′Hcos∠A′HC=
,A′O=
,
∴五棱锥A′-BCDFE的体积V=
×(62-
×4×4)×
=
.
 (1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,
(1)证明:连接AC,设AC∩EF=H,连接A′H,则EF⊥AC,EF⊥A′H,∵AC∩A′H=H,
∴EF⊥平面A′HC,
∵A′C⊂平面A′HC,
∴A′C⊥EF;
(2) 由ABCD是正方形,AE=AF=4,
得H是EF的中点,
且EF⊥AH,EF⊥CH,
从而有A′H⊥EF,CH⊥EF,
∴EF⊥平面A′HC,
从而平面A′HC⊥平面ABCD,
过点A′作A′O垂直HC且与HC相交于点O,
则A′O⊥平面ABCD.
∵正方形ABCD的边长为6,AE=AF=4,
得到:A′H=2
| 2 |
| 2 |
∴cos∠A′HC=
| 8+32-24 | ||||
2×2
|
| 1 |
| 2 |
∴HO=A′Hcos∠A′HC=
| 2 |
| 6 |
∴五棱锥A′-BCDFE的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
28
| ||
| 3 |
看了 如图,已知正方形ABCD的边...的网友还看了以下:
1.n阶方阵,A,B满足AB=A+B,且A-E可逆,求(A-E)^-1=2.如果2阶矩阵A的特征值 2020-04-12 …
(“*”为未知数x)e*/a+a/e*=1/ae*+ae*为什么会等于(a-1/a)(1/e*-e 2020-06-07 …
设A与A+E均可逆,G=E-(A+E)^-1,则G^-1= 2020-06-12 …
设A=(101;020;-101)求满足方程AB+E=A^2+B的矩阵B用AB+E=A^2+B(A 2020-06-18 …
设矩阵A,B满足A=E(1,3)E(5(-2))BE(3,2(1/2)),则有A.B=E(1,3) 2020-06-28 …
设A是2阶方阵,且A^2=E,A不等于±E,证明:r(A+E)=r(A-E)=1 2020-11-02 …
线性代数问题(A-E)^-1=?设n阶方阵A满足A^+4A-8E=0,且A-E可逆,则(A-E)^- 2020-11-18 …
也是椭圆的.a(a+ex0)=c(a-ex0)是怎么变成x0=[a(e-1)]/[e(e=1)]的? 2020-12-03 …
已知地球运行的轨道是长半轴长a=1.50*10^8km,离心率e=0.0192的椭圆,且太阳在这个椭 2021-01-16 …
求逆矩阵1).若A是n阶方阵且满足A^2=A,且矩阵A+E可逆,则(A+E)^-1=?答案是-1/2 2021-02-05 …