早教吧作业答案频道 -->数学-->
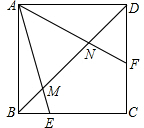
正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.
题目详情
正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.

▼优质解答
答案和解析
证明:延长CB到G,使BG=DF,连接AG,在AG截取AH=AN,连接MH、BH,如图所示: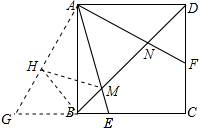
∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠BDC=∠ABD=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,∠AFD=∠G,AF=AG,
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°=∠EAF,
在△AMN和△AMH中,
,
∴△AMN≌△AMH(SAS),
∴MN=MH,
∵AF=AG,AN=AH,
∴FN=AF-AN=AG-AH=GH,
在△DFN和△BGH中,
,
∴△DFN≌△BGH(SAS),
∴∠GBH=∠NDF=45°,DN=BH,
∴∠MBH=∠ABH+∠ABD=∠ABG-∠GBH+∠ABD=90°-45°+45°=90°,
∴BM2+DN2=BM2+BH2=MH2=MN2,
∴DN、BM、MN为三边的三角形为直角三角形.

∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠BDC=∠ABD=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°,
在△ABG和△ADF中,
|
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,∠AFD=∠G,AF=AG,
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°=∠EAF,
在△AMN和△AMH中,
|
∴△AMN≌△AMH(SAS),
∴MN=MH,
∵AF=AG,AN=AH,
∴FN=AF-AN=AG-AH=GH,
在△DFN和△BGH中,
|
∴△DFN≌△BGH(SAS),
∴∠GBH=∠NDF=45°,DN=BH,
∴∠MBH=∠ABH+∠ABD=∠ABG-∠GBH+∠ABD=90°-45°+45°=90°,
∴BM2+DN2=BM2+BH2=MH2=MN2,
∴DN、BM、MN为三边的三角形为直角三角形.
看了 正方形ABCD中,∠EAF=...的网友还看了以下:
已知A、B、C、D、E、F是含有同一种元素的化合物,其中F是能使湿润红色石蕊试纸变蓝的气体,它们之 2020-05-02 …
第一题令A={a,b,c,d,e},B={a,b,c,d,e,f,g,h}.求a)A∪Bb)A∩B 2020-06-17 …
求理由.下列等式正确的是A.∫f'(x)dx=f(x)B.d∫f(x)dx=f(x)C.∫df(x 2020-07-01 …
求光栅常数d一束具有两种波长a和d的平行光垂直照射到一衍射光栅上,测得波长a的第三极主极大衍射角和 2020-07-10 …
已知集合A{a,b,c,d,e},B{0,1,…2014},f为A→B映射,且满足f(已知集合A{ 2020-07-30 …
绕弯的题,我被绕晕了,求函数有七组数据,ABCDEFG,已知A,B,C,七组数据的关系D+E=B,F 2020-11-11 …
已知关系模式R=(A,B,C,D,E,F,G)满足.求R的码已知关系模式R=(A,B,C,D,E,F 2020-11-19 …
有含钠元素的两种物质A和B,它们与化合物F的反应分别是A+F→C+D↑;B+F→C+E↑,又知常温下 2020-12-02 …
已知f(x)在R上是增函已知f(x)在R上是增函数,a,b∈R,且a+b≤0,则有[]A、f(a)+ 2020-12-08 …
若f(x)在(c,d)区间内存在二阶导数,a,b∈(c,d),且f'(a)=0.证明:在(a,b)内 2020-12-28 …