早教吧作业答案频道 -->数学-->
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?(2)
题目详情
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
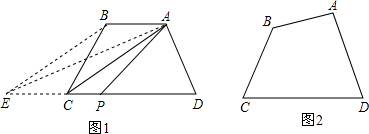 (1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
 四边形ABCD=△ADE
四边形ABCD=△ADE
△ADC△ABC

(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
 (1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
 四边形ABCD=△ADE
四边形ABCD=△ADE△ADC△ABC

▼优质解答
答案和解析
(1)如图1中,∵AB∥EC,AB=EC,
∴四边形ABEC是平行四边形,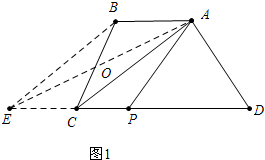
∴BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
S△AED=
S梯形ABCD,
∴直线AP平分梯形ABCD的面积.
(2)如图2中,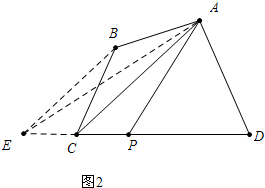 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
S△AED=
S梯形ABCD.
1 2 1 1 12 2 2S△AED△AED=
S梯形ABCD,
∴直线AP平分梯形ABCD的面积.
(2)如图2中, 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
S△AED=
S梯形ABCD.
1 2 1 1 12 2 2S梯形ABCD梯形ABCD,
∴直线AP平分梯形ABCD的面积.
(2)如图2中, 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
∵BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
S△AED=
S梯形ABCD.
1 2 1 1 12 2 2S△AED△AED=
S梯形ABCD.
1 2 1 1 12 2 2S梯形ABCD. 梯形ABCD.
∴四边形ABEC是平行四边形,

∴BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
| 1 |
| 2 |
| 1 |
| 2 |
∴直线AP平分梯形ABCD的面积.
(2)如图2中,
 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴直线AP平分梯形ABCD的面积.
(2)如图2中,
 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴直线AP平分梯形ABCD的面积.
(2)如图2中,
 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:∵BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
看了 (1)如图(1),在四边形A...的网友还看了以下:
已知非零向量e1,e2不共线,如果AB=e1+e2,AC=2e1+8e2,AD=3e1-3e2,求 2020-05-13 …
证明空间中的四点A,B,C,D共面的充分必要条件是它们所对应的位置向量a,b,c,d满足(d,b, 2020-05-13 …
已知平面六面体ABCD-A'B'C'D',点M是棱AA'的中点,点G在对角A'C线上且CG:GA' 2020-05-13 …
已知在平面直角坐标系中直线AB,CD分别与X轴,Y轴交于A,B,C,D,点A(-2,0)B(0,3 2020-05-15 …
如图,把四边形ABCD的各边都延长一倍至A′B′C′D′,连接这些点得新四边形A′B′C′D′,若 2020-06-13 …
读图,根据图中信息,判断下面说法正确的是()A.小溪的流向是自东南向西北流B.从C点爬到山顶A比从 2020-07-11 …
已知长方体ABCD-A'B'C'D',点E,F分别是上底面A'B'C'D'和平面CC'D'D的中心 2020-07-31 …
在长方体ABCD-A'B'C'D',底面是边长为2的正方形,高为4,则点A'到截面AB'D'的距离 2020-08-02 …
四边形ABCD的各边都延长一倍至A'B'C'D',连接这些点得到一个新的四边形A'B'C'D'.若四 2020-11-10 …
如图,已知扇形aob的半径为2,圆心角为90度,点c动点,面积的最大值如图,已知扇形aob的半径为2 2020-12-05 …