早教吧作业答案频道 -->数学-->
在半圆O中,AB为直径,弦AD、BC交于E,连接CD,∠C+2∠D=90°.(1)如图1,求证:弧AC=弧CD;(2)如图2,点F为劣弧BD上一点,连接OF交BC于G,连接BF,若∠CBF=45°,求证:BG=EG;(3)如图3,在
题目详情
在半圆O中,AB为直径,弦AD、BC交于E,连接CD,∠C+2∠D=90°.
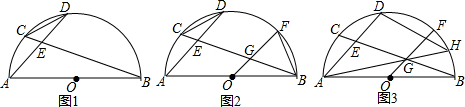
(1)如图1,求证:弧AC=弧CD;
(2)如图2,点F为劣弧BD上一点,连接OF交BC于G,连接BF,若∠CBF=45°,求证:BG=EG;
(3)如图3,在(2)的条件下,连接AG并延长与 O相交于点H,连接DH,若HG=5,DH=9,求线段BE的长度.

(1)如图1,求证:弧AC=弧CD;
(2)如图2,点F为劣弧BD上一点,连接OF交BC于G,连接BF,若∠CBF=45°,求证:BG=EG;
(3)如图3,在(2)的条件下,连接AG并延长与 O相交于点H,连接DH,若HG=5,DH=9,求线段BE的长度.
▼优质解答
答案和解析
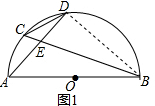 (1)连接BD,
(1)连接BD,
∵AB为 O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠C+2∠D=90°,∠A=∠C,
∴∠ABD=2∠ADC,
∵∠ADC=∠ABC,
∴∠ABC=∠CBD,
∴
=
;
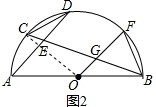
(2)连接OC,
∵∠CBF=45°,
∴∠COF=90°,
∵
=
,
∴OC⊥AD,
∴AD∥OF,
∵AO=BO,
∴BG=EG;
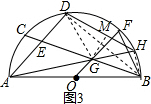
(3)连接BD,DG,作GM⊥DH于M,
∵AB为 O的直径,
∴∠ADB=90°,
∵BG=EG,
∴DG=BG,
∵∠GDM=∠GDB+∠BDH,∠BGH=∠GBA+∠HAB,
∵∠BDH=∠BAH,∠GDB=∠GBD,
∴∠GDM=∠BGH,
在△DGM与△BGH中,
,
∴△DGM≌△BGH,
∴DM=HG,
∵HG=5,DH=9,
∴MH=4,
∴MG=
=3,
∴DG=
=
,
∴BG=DG=
,
∴BE=2BG=2
.
 (1)连接BD,
(1)连接BD,∵AB为 O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠C+2∠D=90°,∠A=∠C,
∴∠ABD=2∠ADC,
∵∠ADC=∠ABC,
∴∠ABC=∠CBD,
∴
 |
| AC |
 |
| CD |

(2)连接OC,
∵∠CBF=45°,
∴∠COF=90°,
∵
 |
| AC |
 |
| CD |
∴OC⊥AD,
∴AD∥OF,
∵AO=BO,
∴BG=EG;

(3)连接BD,DG,作GM⊥DH于M,
∵AB为 O的直径,
∴∠ADB=90°,
∵BG=EG,
∴DG=BG,
∵∠GDM=∠GDB+∠BDH,∠BGH=∠GBA+∠HAB,
∵∠BDH=∠BAH,∠GDB=∠GBD,
∴∠GDM=∠BGH,
在△DGM与△BGH中,
|
∴△DGM≌△BGH,
∴DM=HG,
∵HG=5,DH=9,
∴MH=4,
∴MG=
| GH2-MH2 |
∴DG=
| DM2+MG2 |
| 34 |
∴BG=DG=
| 34 |
∴BE=2BG=2
| 34 |
看了 在半圆O中,AB为直径,弦A...的网友还看了以下:
已知函数f(x)=b*a^x(其中a,b为常量且a>0,a不等于1)的图像经过点A(1,6),B( 2020-04-05 …
现规定一种运算:a现规定一种运算a※b=a的平方b,其中a,b为实数,则2a的平方b+(b-a)※ 2020-05-13 …
已知函数f(x)=ax+b,当x属于[a1,b1]时,f(x)的值域为[a2,b2],当x属于[a 2020-06-02 …
已知函数f(x)=ax+b,当x属于[a1,b1]时,f(x)的值域为[a2,b2],当x属于[a 2020-06-02 …
因式分解的题...2x-3/x^2-x=A/x-1+B/x,其中A,B为常数,则A+B的值为?已知 2020-07-20 …
整式A除以整式B,可以表示成AB的形式,如果除式B中含有字母,那么AB会为,其中A称为分式的分子, 2020-07-30 …
整式A除以整式B,可以表示成AB的形式,如果除式B中含有字母,那么AB会为,其中A称为分式的分子, 2020-07-30 …
成都七中的,两个二次项系数不相等的关于x的二次方程(a-1)x^2-(a^2+2)x+(a^2+2 2020-08-01 …
设满足y大于等于Ix-aI的点(x,y)的集合为A,满足y小于等于-IxI+b的点的集合为B,其中 2020-08-02 …
对于x,y定义一种新运算“※”:x※y=ax-by,其中a,b为常数,等式右边是通常的减法和乘法运算 2020-11-01 …