早教吧作业答案频道 -->数学-->
我们将抛物线少y=ax2+bx+c(a≠0)与x轴的一个交点、与y轴的交点及原点三点构成的三角形,称为这条抛物线的“原发三角形”(1)抛物线y=x2-2x+1的“原发三角形”的面积为;(2)当c=时
题目详情
我们将抛物线少y=ax2+bx+c(a≠0)与x轴的一个交点、与y轴的交点及原点三点构成的三角形,称为这条抛物线的“原发三角形”
(1)抛物线y=x2-2x+1的“原发三角形”的面积为___;
(2)当c=___时,抛物线y=(x-1)(x-c)(其中c≠0和1)的两个“原发二角形”全等?
请在图1平面直角坐标系中画出该抛物线的图象,并说明理由;(铅笔画图后请用黑色水笔加浓)
(3)请直接写出抛物线y=x2+4x+c的“原发三角形”的个数及相应的c的取值范围(或值).
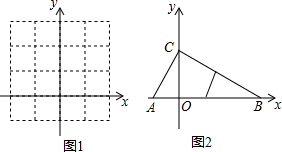
(4)如图2,点B的坐标是(4,0),点C的坐标是(0,2),点A是射线BO上的动点(不与点B,O重合).△AOC和△BOC是抛物线y=ax2+bx+c(a≠0)的两个“原发三角形”.当原点到△ABC的外接圆圆心的距离最小时,求出此时抛物线的解析式.

(1)抛物线y=x2-2x+1的“原发三角形”的面积为___;
(2)当c=___时,抛物线y=(x-1)(x-c)(其中c≠0和1)的两个“原发二角形”全等?
请在图1平面直角坐标系中画出该抛物线的图象,并说明理由;(铅笔画图后请用黑色水笔加浓)
(3)请直接写出抛物线y=x2+4x+c的“原发三角形”的个数及相应的c的取值范围(或值).
(4)如图2,点B的坐标是(4,0),点C的坐标是(0,2),点A是射线BO上的动点(不与点B,O重合).△AOC和△BOC是抛物线y=ax2+bx+c(a≠0)的两个“原发三角形”.当原点到△ABC的外接圆圆心的距离最小时,求出此时抛物线的解析式.
▼优质解答
答案和解析
(1)∵抛物线y=x2-2x+1,
∴抛物线与x轴的交点为B(1,0),与y轴的交点为C(0,1),
∴S=
×1×1=
,
故答案为
(2)∵y=(x-1)(x-c),
∴A(1,0),B(c,0),
∵抛物线y=(x-1)(x-c)(其中c≠0和1)的两个“原发二角形”全等,
∴①△AOC≌△BOC,
∴AO=BO,
∴|c|=1,
∴c=1(舍)或c=-1,
②△AOC≌△COB,
∴AO=CO,
∴∴|c|=1,
∴c=1(舍)或c=-1,
故答案为c=-1
(3)抛物线y=x2+4x+c的“原发三角形”,
∴△=16-4c,
①当△<0时,即:16-4c<0,
∴t>4时,没有原发三角形,
②当△=0时,即:c=4时,只有一个原发三角形,
③当△>0,即:c<4且c≠0时,有两个原发三角形.
(4)∵点B的坐标是(4,0),点C的坐标是(0,2)
∴BC解析式为y=-
x+2,
∴△ABC的外接圆圆心M,
∴M在BC垂直平分线l上,
∴l的解析式为y=2x-3,
∵△ODM∽△CDF,
∴
=
,
∴
=
,
∴OM=
,
根据勾股定理得,DM=
,
∴MF=
,OF=
,
∴M(
,
),
∵M也是AB的垂直平分线,
∴A(-
,0),
∵点A,B(4,0),C(0,2)在抛物线上,
∴y=a(x+
)(x-4),
∴a=-
,
∴y=-
x2+
x+2.
∴抛物线与x轴的交点为B(1,0),与y轴的交点为C(0,1),
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
(2)∵y=(x-1)(x-c),
∴A(1,0),B(c,0),
∵抛物线y=(x-1)(x-c)(其中c≠0和1)的两个“原发二角形”全等,
∴①△AOC≌△BOC,
∴AO=BO,
∴|c|=1,
∴c=1(舍)或c=-1,
②△AOC≌△COB,
∴AO=CO,
∴∴|c|=1,
∴c=1(舍)或c=-1,
故答案为c=-1
(3)抛物线y=x2+4x+c的“原发三角形”,
∴△=16-4c,
①当△<0时,即:16-4c<0,
∴t>4时,没有原发三角形,
②当△=0时,即:c=4时,只有一个原发三角形,
③当△>0,即:c<4且c≠0时,有两个原发三角形.
(4)∵点B的坐标是(4,0),点C的坐标是(0,2)
∴BC解析式为y=-
| 1 |
| 2 |
∴△ABC的外接圆圆心M,
∴M在BC垂直平分线l上,
∴l的解析式为y=2x-3,
∵△ODM∽△CDF,
∴
| OM |
| CE |
| OD |
| CD |
∴
| OM | ||
|
| 3 |
| 5 |
∴OM=
3
| ||
| 5 |
根据勾股定理得,DM=
6
| ||
| 5 |
∴MF=
| 6 |
| 5 |
| 3 |
| 5 |
∴M(
| 6 |
| 5 |
| 3 |
| 5 |
∵M也是AB的垂直平分线,
∴A(-
| 8 |
| 5 |
∵点A,B(4,0),C(0,2)在抛物线上,
∴y=a(x+
| 8 |
| 5 |
∴a=-
| 5 |
| 16 |
∴y=-
| 5 |
| 16 |
| 3 |
| 4 |
看了 我们将抛物线少y=ax2+b...的网友还看了以下:
二次函数的一些题目1..当二次函数图像与x轴交点的横坐标分别是xa=-3,x2=1时,且与y轴交点 2020-05-13 …
直线y=kx+b过y=3x-5与y=-2x+10的交点A,y=kx+b交y轴于B,y=-2x+10 2020-05-16 …
1.直线y=kx+b与x轴交点的横坐标,是一元一次方程的解?如直线y=-x+1与x轴交点横坐标即x 2020-05-19 …
初二反比函数题!急!1.已知一次函数y=3x-a的图像与反比例函数y=b-3/x相交,其中一个交点 2020-05-20 …
求圆与一条直线的两个交点的坐标,已知两交点的y轴坐标,并且两交点的y轴相同.现只需求出x1,x2的 2020-06-03 …
判断下列二次函数的图象与x轴有无交点,如有,求出交点的坐标;如没有,请说明理由.(1)y=x平方判 2020-06-14 …
函数1.已知直线y=-2x+6上点A的横坐标为2,直线y=kx+b经过点A与x轴交于点B(1/2, 2020-06-14 …
已知直线m经过两点(1,6)(-3,-2),他和x轴、y轴的交点是B,A,直线n过点(2,-2)且 2020-06-21 …
a为何值时,抛物线y^2=x+a和x^2=y+a有四个交点?证明当这两条抛物线有四个交点时,这四个 2020-07-21 …
急已知C:x^2+(y-1/2)^2=r^2与y=sin(x)的图像有唯一交点,且交点的横坐标为a 2020-07-31 …