如图，在△ABC中，∠B=∠C=36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是（）A.BDBC=5-12B.AD，AE将∠BAC三等分C.△ABE≌

Question

如图，在△ABC中，∠B=∠C=36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是（　　）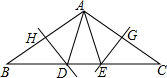

A.

(BD)/(BC)=(√(5)-1)/(2)

B. AD，AE将∠BAC三等分

C. △ABE≌△ACD

D. S_△ADH=S_△CEG

Answer 1

∵∠B=∠C=36°，
∴AB=AC，∠BAC=108°，
∵DH垂直平分AB，EG垂直平分AC，
∴DB=DA，EA=EC，
∴∠B=∠DAB=∠C=∠CAE=36°，
∴△BDA∽△BAC，
∴(BD)/(BA)=(BA)/(BC)，
又∵∠ADC=∠B+∠BAD=72°，∠DAC=∠BAC-∠BAD=72°，
∴∠ADC=∠DAC，
∴CD=CA=BA，
∴BD=BC-CD=BC-AB，
则(BC-BA)/(BA)=(BA)/(BC)=(√(5)-1)/(2)，即(BD)/(BA)=(BA)/(BC)=(√(5)-1)/(2)，故A错误；

∵∠BAC=108°，∠B=∠DAB=∠C=∠CAE=36°，
∴∠DAE=∠BAC-∠DAB-∠CAE=36°，
即∠DAB=∠DAE=∠CAE=36°，
∴AD，AE将∠BAC三等分，故B正确；

∵∠BAE=∠BAD+∠DAE=72°，∠CAD=∠CAE+∠DAE=72°，
∴∠BAE=∠CAD，
在△BAE和△CAD中，
∵

∠B=∠C

AB=AC

∠BAE=∠CAD

，
∴△BAE≌△CAD，故C正确；

由△BAE≌△CAD可得S_△BAE=S_△CAD，即S_△BAD+S_△ADE=S_△CAE+S_△ADE，
∴S_△BAD=S_△CAE，
又∵DH垂直平分AB，EG垂直平分AC，
∴S_△ADH=(1)/(2)S_△ABD，S_△CEG=(1)/(2)S_△CAE，
∴S_△ADH=S_△CEG，故D正确．
故选：A．