如图，在△ABC中，AB=BC，∠ABC=90°，BM是AC边中线，点D，E分别在边AC和BC上，DB=DE，EF⊥AC于点F，以下结论：（1）∠DBM=∠CDE；（2）S△BDE<S四边形BMFE；（3）CD•EN=BN•BD；（4）AC=2DF．其中正

Question

如图，在△ABC中，AB=BC，∠ABC=90°，BM是AC边中线，点D，E分别在边AC和BC上，DB=DE，EF⊥AC于点F，以下结论：
（1）∠DBM=∠CDE； （2）S_△BDE<S_{四边形BMFE}；
（3）CD•EN=BN•BD； （4）AC=2DF．
其中正确结论的个数是（　　）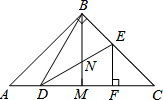

A. 1

B. 2

C. 3

D. 4

Answer 1

（1）设∠EDC=x，则∠DEF=90°-x
∴∠DBE=∠DEB=∠EDC+∠C=x+45°，
∵BD=DE，
∴∠DBM=∠DBE-∠MBE=45°+x-45°=x．
∴∠DBM=∠CDE，故（1）正确；
（2）在Rt△BDM和Rt△DEF中，

∠DBM=∠CDE

∠DMB=∠DFE

BD=DE

，
∴Rt△BDM≌Rt△DEF．
∴S_△BDM=S_△DEF．
∴S_△BDM-S_△DMN=S_△DEF-S_△DMN，即S_△DBN=S_{四边形MNEF}．
∴S_△DBN+S_△BNE=S_{四边形MNEF}+S_△BNE，
∴S_△BDE=S_{四边形BMFE}，故（2）错误；
（3）∵∠BNE=∠DBM+∠BDN，∠BDM=∠BDE+∠EDF，∠EDF=∠DBM，
∴∠BNE=∠BDM．
又∵∠C=∠NBE=45°
∴△DBC∽△NEB．
∴(CD)/(BD)=(BN)/(EN)，
∴CD•EN=BN•BD；故（3）正确；
（4）∵Rt△BDM≌Rt△DEF，
∴BM=DF，
∵∠B=90°，M是AC的中点，
∴BM=(1)/(2)AC．
∴DF=(1)/(2)AC，故（4）正确．
故选：C．