早教吧作业答案频道 -->数学-->
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且BEAB=14.(1)求线段BD的长;(2)求∠ADC的正切值.
题目详情
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且
=
.
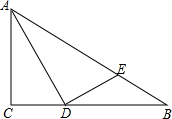
(1)求线段BD的长;
(2)求∠ADC的正切值.
| BE |
| AB |
| 1 |
| 4 |

(1)求线段BD的长;
(2)求∠ADC的正切值.
▼优质解答
答案和解析
(1)∵DE⊥AD,
∴∠BDE=∠CAD=90°-∠CDA,
∵∠CAD=∠DAB,
∴∠BAD=∠BDE,
∵∠B=∠B,
∴△BED∽△BDA,
∴BD2=BE•BA,
∵AB=4,
=
,
∴BE=1,
∴BD2=1×4=4,
∴BD=2;
(2),∵DE⊥AD,
∴∠AED=90°-∠DAE,
∵∠ADE=90°-∠CAD,
∵∠CAD=∠DAB,
∴∠ADE=∠AED,
∵△BED∽△BDA,
∴
=
,
∴tan∠ADC=tan∠AED=
=
=
=2.
∴∠BDE=∠CAD=90°-∠CDA,
∵∠CAD=∠DAB,
∴∠BAD=∠BDE,
∵∠B=∠B,
∴△BED∽△BDA,
∴BD2=BE•BA,
∵AB=4,
| BE |
| AB |
| 1 |
| 4 |
∴BE=1,
∴BD2=1×4=4,
∴BD=2;
(2),∵DE⊥AD,
∴∠AED=90°-∠DAE,
∵∠ADE=90°-∠CAD,
∵∠CAD=∠DAB,
∴∠ADE=∠AED,
∵△BED∽△BDA,
∴
| AD |
| AE |
| AB |
| BD |
∴tan∠ADC=tan∠AED=
| AD |
| AE |
| AB |
| BD |
| 4 |
| 2 |
看了 已知,如图,在Rt△ABC中...的网友还看了以下:
设集合A={a,a²,b²-1}B={0,|a|,b},且A=B 求a,b值设集合A={a,a², 2020-04-05 …
公务员假言命题逻辑:如果A评优了,那么B和C也能评优.为什么是"A→B且C"而不是"A→B或C"公 2020-05-16 …
能判定△ABC与△A'B'C'相似的条件是( )A.A'B'分之AB=A'C'分之AC B. 2020-05-16 …
如图,已知直线a‖b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为如图,已 2020-05-16 …
充分必要与当且仅当有差别吗?这个问题困扰我多年了,今天才提出来.A是B的充分必要条件表示:A->B 2020-06-16 …
一个三位自然数abc的百位,十位,个位上的数字依次为a,b,c,当且仅当a<b且c<b时称为“凸数 2020-07-29 …
设A.B是非空集合,定义A×B={X|X∈A∪B,且X不属于A∩B}.已知A={y|y=√3+2设 2020-08-01 …
在空间直角坐标系中,若向量a→=(−2,1,3),b→=(1,−1,1),c→=(1,−12,−32 2020-11-02 …
已知两条直线a、b及平面α有四个命题:①若a∥b且a∥α则b∥α;②若a⊥α且b⊥α则a∥b;③若a 2020-11-02 …
已知直线a,b和平面α,下列推理错误的是()A.a⊥α且b⊂α⇒a⊥bB.a∥b且a⊥α⇒b⊥αC. 2020-12-23 …