早教吧作业答案频道 -->数学-->
问题情境:如图1,在菱形ABCD中,点E、F分别为AB,BC边上的点,连接AF,DE相交于点O,且∠AOE=∠ADC,试探究:AF与DE的数量关系.特例探究:如图2,当菱形ABCD是正方形时,AF与DE有怎样的数量
题目详情
问题情境:
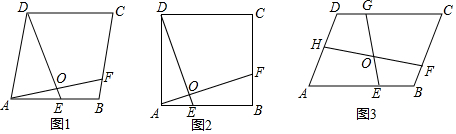
如图1,在菱形ABCD中,点E、F分别为AB,BC边上的点,连接AF,DE相交于点O,且∠AOE=∠ADC,试探究:AF与DE的数量关系.
特例探究:
如图2,当菱形ABCD是正方形时,AF与DE有怎样的数量关系呢?请你直接写出结论,不必证明;
类比解答:
类比特例探究的结论,猜想问题情境中AF与DE的数量关系,并说明理由;
拓展延伸:
将图1中的菱形ABCD改为▱ABCD(如图3)其中AB=a,AD=b,点E、F、G、H分别为AB、BC、CD、DA边上的动点,连接EG、HF相交于点O,且∠HOE=∠ADC,试探究:EG与FH的数量关系,用含a、b的式子直接写出
的值,不必说明理由.
如图1,在菱形ABCD中,点E、F分别为AB,BC边上的点,连接AF,DE相交于点O,且∠AOE=∠ADC,试探究:AF与DE的数量关系.
特例探究:
如图2,当菱形ABCD是正方形时,AF与DE有怎样的数量关系呢?请你直接写出结论,不必证明;
类比解答:
类比特例探究的结论,猜想问题情境中AF与DE的数量关系,并说明理由;
拓展延伸:
将图1中的菱形ABCD改为▱ABCD(如图3)其中AB=a,AD=b,点E、F、G、H分别为AB、BC、CD、DA边上的动点,连接EG、HF相交于点O,且∠HOE=∠ADC,试探究:EG与FH的数量关系,用含a、b的式子直接写出
| EG |
| FH |

▼优质解答
答案和解析
 (1)特例探究:AF=DE.
(1)特例探究:AF=DE.
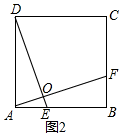
理由:如图2,∵四边形ABCD是正方形,
∴AD=BA,∠DAE=∠B=90°,
∵∠AOE=∠ADC=90°,
∴∠ADE+∠DAO=∠BAF+∠DAO=90°,
∴∠ADE=∠BAF,
∴在ADE和△BAF中,
,
∴△ADE≌△BAF(ASA),
∴AF=DE;
(2)类比AF与DE的数量关系为AF=DE.
理由:如图1,在AB上取点M使得DM=DA,连接DM,交AF于N,则
∠DAM=∠DMA,DM=AD=AB,
∵∠DAB+∠B=180°,∠DMA+∠DME=180°,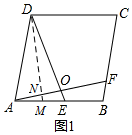
∴∠DME=∠B,
∵∠AOE=∠ADC,
∴∠ADO+∠DAO=∠ADO+∠CDO,
∴∠DAO=∠CDO,
又∵CD∥AB,AD∥BC,
∴∠CDO=∠MED,∠DAO=∠BFA,
∴∠MED=∠BFA,
在△MED和△BFA中,
,
∴△MED≌△BFA(AAS),
∴AF=DE;
(3)拓展延伸:
=
.
如图3,过G作GM⊥AB于M,过H作HN⊥BC于N,
∵四边形ABCD是平行四边形,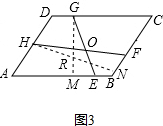
∴AD∥BC,DC∥AB,
∵平行四边形ABCD的面积=AB×GM=BC×HN,
∵AB=a,AD=b,
∴
=
,
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∴△GME∽△HNF,
∴
=
=
.
 (1)特例探究:AF=DE.
(1)特例探究:AF=DE.理由:如图2,∵四边形ABCD是正方形,
∴AD=BA,∠DAE=∠B=90°,
∵∠AOE=∠ADC=90°,
∴∠ADE+∠DAO=∠BAF+∠DAO=90°,
∴∠ADE=∠BAF,
∴在ADE和△BAF中,
|
∴△ADE≌△BAF(ASA),
∴AF=DE;
(2)类比AF与DE的数量关系为AF=DE.
理由:如图1,在AB上取点M使得DM=DA,连接DM,交AF于N,则
∠DAM=∠DMA,DM=AD=AB,
∵∠DAB+∠B=180°,∠DMA+∠DME=180°,

∴∠DME=∠B,
∵∠AOE=∠ADC,
∴∠ADO+∠DAO=∠ADO+∠CDO,
∴∠DAO=∠CDO,
又∵CD∥AB,AD∥BC,
∴∠CDO=∠MED,∠DAO=∠BFA,
∴∠MED=∠BFA,
在△MED和△BFA中,
|
∴△MED≌△BFA(AAS),
∴AF=DE;
(3)拓展延伸:
| EG |
| FH |
| b |
| a |
如图3,过G作GM⊥AB于M,过H作HN⊥BC于N,
∵四边形ABCD是平行四边形,

∴AD∥BC,DC∥AB,
∵平行四边形ABCD的面积=AB×GM=BC×HN,
∵AB=a,AD=b,
∴
| GM |
| HN |
| b |
| a |
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∴△GME∽△HNF,
∴
| EG |
| FH |
| GM |
| HN |
| b |
| a |
看了 问题情境:如图1,在菱形AB...的网友还看了以下:
如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tanB=2.;(3)请你在图 2020-05-13 …
探究影响电流做功多少的因素.(1)电功的多少与多个因素有关,要探究与其中探究影响电流做功多少的因素 2020-05-13 …
等腰直角三角形ABC中,角BAC=90度,AB=AC,AN是经过点A的任意一条直线,BD垂直于AN 2020-06-05 …
已知:△ABC、△DEF均为等边三角形,连接AF.(1)如图1,点C与点E重合时,求证:∠AED= 2020-06-18 …
如图所示的情景,是研究蒸发快慢与哪些因素有关的探究过程,这个探究方案中①图(a)是研究蒸发快慢与液 2020-06-18 …
△ABC中,BF垂直AC,CG垂直AB,垂足分别是F、G,D是BC的中点,DE垂直FG,垂足是E. 2020-06-27 …
小邦利用图所示的器材探究“浮力大小与哪些因素有关”(1)选择器材a、b、d、e探究“浮力的大小是否 2020-07-02 …
探索与发现探索:如图,在直角坐标系中,正方形ABCO的点B坐标(4,4),点A、C分别在y轴、x轴 2020-07-19 …
为了探究浮力的相关规律,小明进行了如下探究:(1)比较四幅图,可知浮力大小等于物体排开液体所受的重力 2020-11-03 …
函数的对称函数y=-e^x的图象1.与y=e^x的图象关于y轴对称2.与y=e^x的图象关于坐标原点 2020-11-11 …