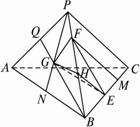
如图，在正三棱锥P—ABC中，三条侧棱两两互相垂直，G是△PAB重心，E、F分别在BC、PB上，且.求证：（1）平面GEF⊥平面PBC；（2）GE是PG与BC的公垂线段.

Question

如图，在正三棱锥 P — ABC 中，三条侧棱两两互相垂直，G是△ PAB 重心， E 、 F 分别在 BC 、 PB 上，且 .

求证：（1）平面G EF ⊥平面 PBC ；

（2）G E 是 P G与 BC 的公垂线段.

Answer 1

证明：（1）连结 B G，延长交 PA 于点 Q .

由 ，可证明G F ∥ PA ，而 PA ⊥平面 PBC ，∴G F ⊥平面 PBC ，G F 平面 EF G.∴平面G EF ⊥平面 PBC .

（2）作 FM ∥ PC 交 BC 于 M ，

∴ ，可得 BE = EM = MC .

又 FM = FB = PC ，

∴在等腰△ FBM 中，

可证 FE ⊥ BM ，由三垂线定理可证 BC ⊥G E .

在△ PCB 中，作 E H⊥ PB 于H，由平面 PBC ⊥平面 PAB ，

可证 E H⊥平面 PAB ，∴ E H∥ PC .

∴ .

设 P G∩ AB = N ，则 .

∴ ，HG∥ BN .

又 PN ⊥ BN ，∴HG⊥ PN .

由三垂线定理可证 P G⊥G E .

∴G E 与 P G、 BC 垂直且相交，则G E 是 P G和 BC 的公垂线段.