如图，在七面体ABCDMN中，四边形ABCD是边长为2的正方形，平面ABCD，平面ABCD，且（1）在棱AB上找一点Q，使QP//平面AMD，并给出证明；（2）求平面BNC与平面MNC所成锐二面角的余

Question

如图，在七面体ABCDMN中，四边形ABCD是边长为2的正方形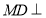， 平面ABCD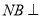， 平面ABCD，且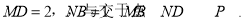

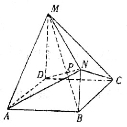
（1）在棱AB上找一点Q，使QP//平面AMD，并给出证明；

（2）求平面BNC与平面MNC所成锐二面角的余弦值.

 

Answer 1

（1）当时，有//平面AMD.证明：因为MD平面ABCD，NB平面ABCD，所以MD//NB，所以，又，所以，所以在中，OP//AM.又面AMD，AM面AMD，∴// 面AMD.（2）锐二面角的余弦值为.

分 析：
（1）设Q为AB上的一点，满足.由线面平行的性质证出MD//NB，结合题中数据利用平行线的性质，得到，从而在中得到OP//AM.最后利用线面平行判定定理，证出// 面AMD，说明在棱AB上存在满足条件的点；（2）建立如图所示空间直角坐标系，算出向量、和的坐标.利用垂直向量数量积为0的方法建立方程组，算出平面CMN的法向量.根据线面垂直的判定定理证出DC平面BNC，从而得到即是BNC的法向量，最后利用空间向量的夹角公式加以计算，即可算出平面CMN与平面BNC所成锐二面角的余弦值.试题
解析：
（1）当时，有//平面AMD.证明：因为MD平面ABCD，NB平面ABCD，所以MD//NB，所以，又，所以，所以在中，OP//AM.又面AMD，AM面AMD，∴// 面AMD.（2）以DA、DC、DM所在直线分别为x轴、y轴、z轴，建立空间直角坐标系，则D（0，0，0），B（2，2，0），C（0，2，0），M（0，0，2）N（2，2，1），所以=（0，-2，2），=（2，0，1），=（0，2，0），设平面CMN的法向量为=（x，y，z）则，所以，所以=（1，-2，-2）.又NB平面ABCD，∴NBDC，BCDC，∴DC平面BNC，∴平面BNC的法向量为==（0，2，0），设所求锐二面角为，则.
考点：
利用空间向量求平面间的夹角；直线与平面平行的判定.