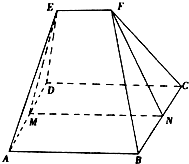
一个楔子形状几何体的直观图如图所示，其底面ABCD为一个矩形，其中AB=6，AD=4，顶部线段EF∥平面ABCD，棱EA=ED=FB=FC=62，二面角F-BC-A的余弦值为1717．设M，N分别是AD，BC的中点．（I）证明：平面

Question

一个楔子形状几何体的直观图如图所示，其底面ABCD为一个矩形，其中AB=6，AD=4，顶部线段EF∥平面ABCD，棱EA=ED=FB=FC=6√(2)，二面角F-BC-A的余弦值为(√(17))/(17)．设M，N分别是AD，BC的中点．
（I）证明：平面EFNM⊥平面ABCD；
（Ⅱ）求直线BF与平面EFCD所成角的正弦值．

Answer 1

（I）证明：∵EF∥平面ABCD，且EF⊂平面EFAB，
又∵平面ABCD∩平面EFAB=AB，
∴EF∥AB，
又M，N是平行四形ABCD两边AD，BC的中点，
∴MN∥AB，
∴EF∥MN，
∴E，F，M，N四点共面．
∵FB=FC，
∴BC⊥FN，
又∵BC⊥AB，
∴BC⊥MN，
∵FN∩MN=N，
∴BC⊥平面EFNM，
∵BC⊂平面ABCD，
∴平面EFNM⊥平面ABCD；
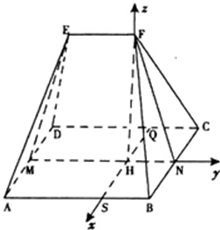
（Ⅱ） 在平面EFNM内F做MN的垂线，垂足为H，则由第（I）问可知：BC⊥平面EFNM，则平面ABCD⊥平面EFNM，∴FH⊥平面ABCD，
又∵FN⊥BC，HN⊥BC，∴二面角F-BC-A的平面角为∠FNH．
在Rt△FNB和Rt△FNH中，FN=√(68)，HNHN=FNcos∠FNH=2，∴FH=8，
过H做边AB，CD的垂线，垂足为S，Q，
以H为坐标原点，以HS，HN，HF方向为x，y，z轴正方向，建立空间直角坐标系，
则F（0，0，8），S（2，0，0），C（-2，2，0），D（-2，-4，0），
则

FB

=（2，2，-8），

FC

=（-2，2，-8），

CD

=（0，-6，0）
设平面EFCD的一个法向量为

n

=（x，y，z），
则

-2x+2y-8z=0

-6y=0

，取z=1，得

n

=（-4，0，1），
设直线BF与平面EFCD所成角为θ，则sinθ=(|-8-8|)/(√(2+4+64)•√(16+1))=

4

作业帮用户 2017-02-05

问题解析

（I）根据线面平行的性质定理推断出EF∥AB，又M，N是平行四形ABCD两边AD，BC的中点，推断出MN∥AB，进而可知EF∥MN，推断出E，F，M，N四点共面．根据FB=FC，推断出BC⊥FN，又BC⊥MN，根据线面垂直的判定定理推断出，BC⊥平面EFNM，即可证明平面EFNM⊥平面ABCD；
（Ⅱ）在平面EFNM内F做MN的垂线，垂足为H，则由第 （1）问可知：BC⊥平面EFNM，则平面ABCD⊥平面EFNM，进而可知FH⊥平面ABCD，又因为FN⊥BC，HN⊥BC，可知二面角F-BC-A的平面角为∠FNH．在Rt△FNB和Rt△FNH中，分别求得FN和HN，过H做边AB，CD的垂线，垂足为S，Q，建立空间直角坐标系，由此能求出直线BF与平面EFCD所成角的正弦值．

名师点评

本题考点：

直线与平面所成的角 平面与平面垂直的判定

考点点评：

本题主要考查了空间点，线面的位置关系，空间的角的计算．考查学生的空间想象能力和运算能力．属于中档题．

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议