某企业拟生产一种如图所示的圆柱形易拉罐（上下底面及侧面的厚度不计），易拉罐的体积为108πml．设圆柱的高度为hcm，底面半径半径为rcm，且h≥4r，假设该易拉罐的制造费用仅与其表面积

Question

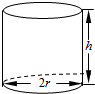
某企业拟生产一种如图所示的圆柱形易拉罐（上下底面及侧面的厚度不计），易拉罐的体积为108πml．设圆柱的高度为hcm，底面半径半径为rcm，且h≥4r，假设该易拉罐的制造费用仅与其表面积有关，已知易拉罐侧面制造费用为m元/cm²，易拉罐上下底面的制造费用均为n元/cm²（m，n为常数）

（1）写出易拉罐的制造费用y（元）关于r（cm）的函数表达式，并求其定义域；
（2）求易拉罐制造费用最低时r（cm）的值．

Answer 1

（1）由题意，体积V=πr²h，得h=(V)/(πr2)=(108)/(r2)．
y=2πrh×m+2πr²×n=2π （(108m)/(r)+nr²）．…（4分）
因为h≥4r，即(108)/(r2)≥4r，所以r≤3，即所求函数定义域为（0，3]．…（6分）
（2）令f（r）=(108m)/(r)+nr²，则f'（r）=-(108m)/(r2)+2nr．
由f'（r）=0，解得r=3

3

(2m)/(n)

．
①若3

3

(2m)/(n)

．<1，当n>2m时，3

3

(2m)/(n)

．∈（0，3]，由

R

（0，3

3

(2m)/(n)

）．

3

3

(2m)/(n)

．

（3

3

(2m)/(n)

．，3]

f'（r）

-

0

+

f（r）

减

增

得，当r=3

3

(2m)/(n)

．时，f（r）有最小值，此时易拉罐制造费用最低．…（10分）
②若3

作业帮用户 2017-05-14

问题解析

（1）由题意，体积V=πr²h，可求得h，再由易拉罐的制造费用公式求得费用，根据函数得意义求得定义域．
（2）利用导数求出函数的单调区间，继而求得函数在定义域内的最值．

名师点评

本题考点：

导数在最大值、最小值问题中的应用

考点点评：

本题主要考查导数在实际应用题中的应用，利用导数求得单调区间求出满足题意的结果．属于中档题型，在高考中时有考查．

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议

3

(2m)/(n)