如图，这是一个半圆柱与多面体ABB1A1C构成的几何体，平面ABC与半圆柱的下底面共面，且AC⊥BC，P为A1B1上的动点．（1）证明：PA1⊥平面PBB1；（2）设半圆柱和多面体ABB1A1C的体积分别为V1，V2，

Question

如图，这是一个半圆柱与多面体ABB₁A₁C构成的几何体，平面ABC与半圆柱的下底面共面，且AC⊥BC，P为

A1B1

上的动点．

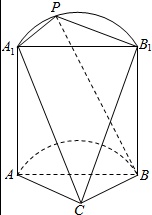
（1）证明：PA₁⊥平面PBB₁；
（2）设半圆柱和多面体ABB₁A₁C的体积分别为V₁，V₂，且AC=BC，求V₁：V₂．

Answer 1

（1）证明：在半圆柱中，BB₁⊥平面PA₁B₁，所以BB₁⊥PA₁．
因为A₁B₁是底面圆的直径，所以PA₁⊥PB₁，因为PB₁∩BB₁=B₁，PB₁⊂平面PBB₁，
BB₁⊂平面PBB₁，所以PA₁⊥平面PBB₁．（6分）
（2） 因为AC⊥BC，AC=BC，所以△ABC是等腰直角三角形，且AB²=BC²+AC²=2AC²．
所以半圆柱的体积V₁=(1)/(2)（(1)/(2)AB）²π•AA₁=(π)/(4)AC²•AA₁．
多面体ABB₁A₁C是以矩形ABB₁A₁为底面，以C为顶点的四棱锥，其高为点C到底面ABB₁A₁的距离，设这个高为h，在Rt△ABC中，AB•h=AC•BC，所以h=(AC•BC)/(AB)，
所以V₂=(1)/(3)•AA₁•AB•(AC•BC)/(AB)=(1)/(3)•AA₁•AC•BC=(1)/(3)AA₁•AC²．
所以(V1)/(V2)=(3π)/(4)．（14分）