如图,已知正三棱锥A―BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.(1)求此正三棱锥的高;(2)求二面角E―FD―B的大小.
如图,已知正三棱锥A―BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.
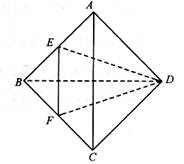
(1)求此正三棱锥的高;
(2)求二面角E―FD―B的大小.
如图,已知正三棱锥A―BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.

(1)求此正三棱锥的高;
(2)求二面角E―FD―B的大小.
如图,已知正三棱锥A―BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.


(1)求此正三棱锥的高;
(2)求二面角E―FD―B的大小.
如果有理数ab满足ab-2的绝对值+1-b的绝对值=0,试求:ab/1 + (a+1)(b+1)/ 2020-04-06 …
已知a−1+(ab-2)2=0,求1ab+1(a+1)(b+1)+1(a+2)(b+2)+…+1( 2020-04-26 …
解分式方程:1.-2乘以(1+1/(A-1))的平方等于A/(A+1),求A2(1/(A-2))- 2020-04-27 …
已知a−1+(ab-2)2=0,求1ab+1(a+1)(b+1)+1(a+2)(b+2)+…+1( 2020-05-21 …
若a,b为实数,且|a-1|+ab−2=0,求1ab+1(a+1)(b+1)+1(a+2)(b+2 2020-06-03 …
an=1/n^2,求Sn原题是这样的:已知a下标(n+1)=a下标(n)+n+1,且a1=1,则数 2020-07-29 …
1.设a+(1/b)=1b+(1/c)=1b不等于1,c不等于1,求c+(1/a)2.设abc=1求 2020-10-31 …
已知:字母a、b满足a-1+b-2=0.求1ab+1(a+1)(b+1)+1(a+2)(b+2)+… 2020-11-07 …
A、B是做匀变速直线运动的两个物体的速度图像,如图1-5-12所示.(1)A、B各做什么运动?求其加 2020-12-09 …
如果有理数a,b满足|ab-2|+(1-b)2=0,试求1ab+1(a+1)(b+1)+1(a+2) 2020-12-31 …