６如图所示的“双塔”形立体建筑，已知是两个高相等的正三棱锥，A、B、D、C在一个平面内.要使塔尖P、Q之间的距离为，则底边AB的长为（）A．
６如图所示的“双塔”形立体建筑，已知
是两个高相等的正三棱锥，A、B、D、C在一个平面内.要使塔尖P、Q之间的距离为
，则底边AB的长为 （ ）
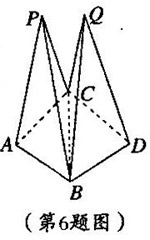A．
B．
C．
D．
６如图所示的“双塔”形立体建筑，已知是两个高相等的正三棱锥，A、B、D、C在一个平面内.要使塔尖P、Q之间的距离为，则底边AB的长为 （ ）
A． B．
C． D．
C
解析:
因为是两个高相等的正三棱锥，所以点P与Q在底面ABC与底面BCD上的射影分别是其中心，所以AD＝３PQ＝９０，得AB＝45÷sin60°=
C
C解析:
因为是两个高相等的正三棱锥，所以点P与Q在底面ABC与底面BCD上的射影分别是其中心，所以AD＝３PQ＝９０，得AB＝45÷sin60°=
是两个高相等的正三棱锥，所以点P与Q在底面ABC与底面BCD上的射影分别是其中心，所以AD＝３PQ＝９０，得AB＝45÷sin60°= 已知等轴双曲线C:x^2-y^2=a^2（a>0)的右焦点F,O为坐标原点.过F作一条渐近线的垂线 2020-05-16 …
一道双曲线题,急,设F1F2分别为双曲线(x^2)/(a^2)-(y^2)/(b^2)=1的左右焦 2020-05-23 …
已知双曲线（b>0），以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A、B、 2020-06-16 …
设F1、F2分别为双曲线x^2/a^2-y^2/b^2=1的左右焦点,若在双曲线右支上存在点P,满 2020-07-16 …
设F1，F2分别为双曲线－＝1(a>0，b>0)的左，右焦点，若在双曲线右支上存在一点P，满足|P 2020-07-30 …
设F1，F2分别为双曲线的左、右焦点，点P在双曲线右支上，旦，F2到直线PF1的距离等于双曲线的实 2020-07-30 …
若双曲线x2a2-y2b2=1（a>0，b>0）的焦点到其渐近线的距离等于实轴长，且P（2，2）为 2020-07-30 …
设F1、F2分别为双曲线x2a2−y2b2＝1(a＞0，b＞0)的左、右焦点.若在双曲线右支上存在 2020-07-30 …
数学圆锥曲线过双曲线的左焦点F引圆x2+y2=a2的切线,切点为A,延长FA交双曲线右支于过双曲线 2020-08-02 …
（2014•闵行区三模）设F1、F2分别为双曲线x2a2−y2b2＝1(a＞0，b＞0)的左、右焦点 2021-01-23 …