在△ABC中，已知AB=8，BC=7，cos（C-A）=1314，则△ABC的面积为．

Question

在△ABC中，已知AB=8，BC=7，cos（C-A）= (13)/(14)，则△ABC的面积为___．在△ABC中，已知AB=8，BC=7，cos（C-A）= (13)/(14)，则△ABC的面积为___． (13)/(14)，则△ABC的面积为___．(13)/(14) 13 14 13 13 14 14

Answer 1

∵AB>BC，∴C>A，
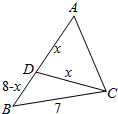
作CD=AD，则∠DCA=∠A，则∠BCD=C-A，
即cos∠BCD=cos（C-A）=(13)/(14)，
设AD=CD=x，则BD=8-x，
在△BDC中，由余弦定理得：BD²=CD²+BC²-2CD•BC•cos∠BCD，
即（8-x）²=x²+49-2×7x•(13)/(14)=x²+49-13x，
即64-16x+x²=x²+49-13x，
即3x=15
解得：x=5，
∴AD=5，BD=3，CD=5
在△BCD中，由余弦定理得cosB=(BD2+BC2-CD2)/(2BD•BC)=(9+49-25)/(2×3×7)=(11)/(14)．
则sinB=√(1-((11)/(14))2)=(5√(3))/(14)，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (13)/(14)1314131313141414，
设AD=CD=x，则BD=8-x，
在△BDC中，由余弦定理得：BD²2=CD²2+BC²2-2CD•BC•cos∠BCD，
即（8-x）²2=x²2+49-2×7x•(13)/(14)=x²+49-13x，
即64-16x+x²=x²+49-13x，
即3x=15
解得：x=5，
∴AD=5，BD=3，CD=5
在△BCD中，由余弦定理得cosB=(BD2+BC2-CD2)/(2BD•BC)=(9+49-25)/(2×3×7)=(11)/(14)．
则sinB=√(1-((11)/(14))2)=(5√(3))/(14)，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (13)/(14)1314131313141414=x²2+49-13x，
即64-16x+x²2=x²2+49-13x，
即3x=15
解得：x=5，
∴AD=5，BD=3，CD=5
在△BCD中，由余弦定理得cosB=(BD2+BC2-CD2)/(2BD•BC)=(9+49-25)/(2×3×7)=(11)/(14)．
则sinB=√(1-((11)/(14))2)=(5√(3))/(14)，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (BD2+BC2-CD2)/(2BD•BC)BD2+BC2-CD22BD•BCBD2+BC2-CD2BD2+BC2-CD2BD2+BC2-CD22+BC2-CD22-CD222BD•BC2BD•BC2BD•BC=(9+49-25)/(2×3×7)=(11)/(14)．
则sinB=√(1-((11)/(14))2)=(5√(3))/(14)，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (9+49-25)/(2×3×7)9+49-252×3×79+49-259+49-259+49-252×3×72×3×72×3×7=(11)/(14)．
则sinB=√(1-((11)/(14))2)=(5√(3))/(14)，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (11)/(14)1114111111141414．
则sinB=√(1-((11)/(14))2)=(5√(3))/(14)，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) √(1-((11)/(14))2)

1-((11)/(14))2

1-((11)/(14))2

1-((11)/(14))21-((11)/(14)1114111111141414)22=(5√(3))/(14)，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (5√(3))/(14)5√(3)145√(3)5√(3)5√(3)

3

3

33141414，
则三角形的面积S=(1)/(2)×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (1)/(2)12111222×7×8×(5√(3))/(14)=10√(3)，
故答案为：10√(3) (5√(3))/(14)5√(3)145√(3)5√(3)5√(3)

3

3

33141414=10√(3)，
故答案为：10√(3) √(3)

3

3

33，
故答案为：10√(3) √(3)

3

3

33