早教吧作业答案频道 -->数学-->
有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
题目详情
有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
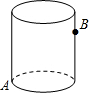 有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)


 有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)

▼优质解答
答案和解析
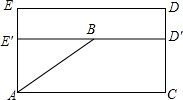 从点A处竖直向上剪开,此圆柱体的侧面展开图如图,其中AC为圆柱体的底面周长,
从点A处竖直向上剪开,此圆柱体的侧面展开图如图,其中AC为圆柱体的底面周长,
则AC=2πr≈2×3×4=24(cm),则E′B=
E′D′=
AC=
×24=12(cm).
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2=52+122=132,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
1 2 1 1 12 2 2E′D′=
AC=
×24=12(cm).
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2=52+122=132,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
1 2 1 1 12 2 2AC=
×24=12(cm).
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2=52+122=132,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
1 2 1 1 12 2 2×24=12(cm).
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB22=AE′22+E′B22=522+1222=1322,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
 从点A处竖直向上剪开,此圆柱体的侧面展开图如图,其中AC为圆柱体的底面周长,
从点A处竖直向上剪开,此圆柱体的侧面展开图如图,其中AC为圆柱体的底面周长,则AC=2πr≈2×3×4=24(cm),则E′B=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2=52+122=132,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2=52+122=132,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
| 1 |
| 2 |
| 1 |
| 2 |
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB2=AE′2+E′B2=52+122=132,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
| 1 |
| 2 |
又∵EA=8cm,EE′=3cm,
∴AE′=EA-EE′=8-3=5(cm).
在Rt△ABE′中,AB22=AE′22+E′B22=522+1222=1322,
∴AB=13(cm),
∵两点之间,线段最短,
∴蚂蚁从A点爬到B点的最短距离为13cm.
看了 有一只蚂蚁要从一个圆柱形玻璃...的网友还看了以下:
圆锥底面半径为R,母线长3R,M是底面圆上一点,从点M拉一条绳子绕圆锥一圈,再回到点M,求M这根绳 2020-06-06 …
汇编中,ModR/M里,R/M具体含义是什么?ModR/M决定操作数的过程中,这个R/M到底表示什 2020-06-08 …
一道类似于斐波那挈数列的数学题一只小猴爬梯,由下向上爬,每次可以爬一级或两级或三级台阶.若梯子有一 2020-06-18 …
给定函数f(x),若对于定义域中的任意x,都有f(x)≥x恒成立,则称函数f(x)为“爬坡函数”. 2020-06-27 …
求教一个有关对数与最值的问题!已知a,b是不相等的正常数,x为自变量,f(x)=以m为底,x/a为 2020-07-19 …
1.已直Lg2=a,lg3=b,试用a,b表示log512(5是底数,12是真数)2.若a+b=( 2020-07-30 …
数学求范围的题函数F(X)=log以3为底,真数位置是4的X幂+4的X幂分之4+m的值域为R.则m 2020-07-30 …
高一数学函数问题(1)利用关系式logaN=b=>a^b=N证明换底公式logaN=logmN/l 2020-07-30 …
已知2X+5Y-4=0,求4^x×32^y若X=2^m+1,y=3+4^m,则用X的代数式表示Y已知 2020-11-27 …
求下列函数的定义域1.y=三次根号下log2x2.y=根号下log0.5(4x-3)已知下列不等式, 2020-11-27 …