早教吧作业答案频道 -->数学-->
我们把a、b、c三个数的中位数记作Z{a,b,c},直线y=kx+12(k>0)与函数y=Z{x,13x+43,-x}的图象有且只有2个交点,则k的取值为.
题目详情
我们把a、b、c三个数的中位数记作Z{a,b,c},直线y=kx+
(k>0)与函数y=Z{x,
x+
,-x}的图象有且只有2个交点,则k的取值为___.我们把a、b、c三个数的中位数记作Z{a,b,c},直线y=kx+
(k>0)与函数y=Z{x,
x+
,-x}的图象有且只有2个交点,则k的取值为___.
(k>0)与函数y=Z{x,
x+
,-x}的图象有且只有2个交点,则k的取值为___.
1 2 1 1 2 2
x+
,-x}的图象有且只有2个交点,则k的取值为___.
1 3 1 1 3 3
,-x}的图象有且只有2个交点,则k的取值为___.
4 3 4 4 3 3
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
▼优质解答
答案和解析
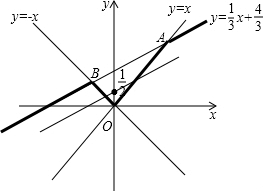 如图,
如图,
图中粗线条代表Z的图象,
将A(2,2)代入,k最大,
当y=kx+
(k>0)与AB平行时,k最小,
∴
≤k≤
.
故答案为:
≤k≤
.
1 2 1 1 12 2 2(k>0)与AB平行时,k最小,
∴
≤k≤
.
故答案为:
≤k≤
.
1 3 1 1 13 3 3≤k≤
.
故答案为:
≤k≤
.
3 4 3 3 34 4 4.
故答案为:
≤k≤
.
1 3 1 1 13 3 3≤k≤
.
3 4 3 3 34 4 4.
 如图,
如图,图中粗线条代表Z的图象,
将A(2,2)代入,k最大,
当y=kx+
| 1 |
| 2 |
∴
| 1 |
| 3 |
| 3 |
| 4 |
故答案为:
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 3 |
| 3 |
| 4 |
故答案为:
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
故答案为:
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
故答案为:
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
看了 我们把a、b、c三个数的中位...的网友还看了以下:
问个数学问题(抽屉原理的)在不超过100的正整数中任取55个不同的数,在这55个数中:(1)是否一 2020-05-16 …
11个数字里会出5个中奖数字我们选7个数字猜中中奖数字中的4个数字的概率是?我们选5个数字猜中中奖 2020-06-10 …
将自然数排列如图,在这个数阵里,小明用正方形框出九个数.(1)任意移动几次,每次框住的9个数和与中 2020-06-18 …
求解问题的方法(不要硬算的)有一列数:1,1,3,8,22,60,164,448,……其中的前3个 2020-07-18 …
有一串数字排成一行,其中第一个数字是3,第二个数字是4,从第三个起,每个数恰好是前两个数的和.在这 2020-07-19 …
先从1至50这50个数里选6个数.另外再从这50个数里选出3个数从1到50这50个数中选6个数,另 2020-07-29 …
表的粗线框一次可以框出5个数,在表中移动这个框.我们把8所处的位置称之为“中心数”.(1)当“中心数 2020-11-06 …
有一列数:1,1,3,8,22,60,164,448.其中的前三个数是1,1,3,从第四个数起,每个 2020-11-20 …
“几个数的平均数必定是这几个数中大小居中的一个.”这句话对吗?“几个数的平均数必定是这几个数中大小居 2020-12-11 …
有2012个数排成一行,其中任意相邻的三个数中,中间的数等于它前后两数的和,若第一个数和第二个数都是 2020-12-23 …