早教吧作业答案频道 -->数学-->
如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转
题目详情
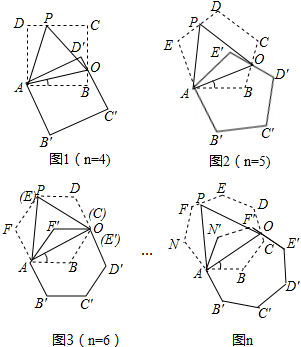
如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是___.(填番号)
①在图1中,△AOB≌△AOD';
②在图2中,正五边形的“叠弦角”的度数为360°;
③“叠弦三角形”不一定都是等边三角形; ④正n边形的“叠弦角”的度数为60°-
.
 如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是___.(填番号)
如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是___.(填番号)
①在图1中,△AOB≌△AOD';
②在图2中,正五边形的“叠弦角”的度数为360°;
③“叠弦三角形”不一定都是等边三角形; ④正n边形的“叠弦角”的度数为60°-
.

.

180° n 180° 180° n n

①在图1中,△AOB≌△AOD';
②在图2中,正五边形的“叠弦角”的度数为360°;
③“叠弦三角形”不一定都是等边三角形; ④正n边形的“叠弦角”的度数为60°-
| 180° |
| n |
 如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是___.(填番号)
如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是___.(填番号)①在图1中,△AOB≌△AOD';
②在图2中,正五边形的“叠弦角”的度数为360°;
③“叠弦三角形”不一定都是等边三角形; ④正n边形的“叠弦角”的度数为60°-
| 180° |
| n |

| 180° |
| n |

| 180° |
| n |

▼优质解答
答案和解析
①∵四边形ABCD是正方形,
∴AB=AD,∠D=∠B=90°,
由旋转的性质得,AD=AD′,∠D=∠D′=90°,
∴AB=AD′,
在Rt△ABO与Rt△AD′O中,
,
∴Rt△ABO≌Rt△AD′O,
故①正确;
②如图2,
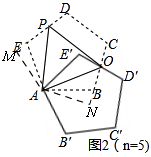
作AM⊥DE于M,作AN⊥CB于N.
∵五边形ABCDE是正五边形,
由旋转知:AE=AE',∠E=∠E'=108°,∠EAE'=∠OAP=60°,
∴∠EAP=∠E'AO,
在△APE与△AOE'中,
,
∴△APE≌△AOE′(ASA),
∴∠OAE′=∠PAE.
在Rt△AEM和Rt△ABN中,
,
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
,
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
(108°-60°)=24°,
故②错误;
③如图3,
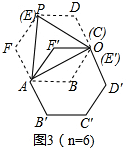
∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
,
故④错误.
故答案:①.
AB=AD′ AO=AO AB=AD′ AB=AD′ AB=AD′AO=AO AO=AO AO=AO
∴Rt△ABO≌Rt△AD′O,
故①正确;
②如图2,

作AM⊥DE于M,作AN⊥CB于N.
∵五边形ABCDE是正五边形,
由旋转知:AE=AE',∠E=∠E'=108°,∠EAE'=∠OAP=60°,
∴∠EAP=∠E'AO,
在△APE与△AOE'中,
,
∴△APE≌△AOE′(ASA),
∴∠OAE′=∠PAE.
在Rt△AEM和Rt△ABN中,
,
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
,
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
(108°-60°)=24°,
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
,
故④错误.
故答案:①.
∠E=∠E′=108° AE=AE′ ∠EAP=∠E′AO ∠E=∠E′=108° ∠E=∠E′=108° ∠E=∠E′=108°AE=AE′ AE=AE′ AE=AE′∠EAP=∠E′AO ∠EAP=∠E′AO ∠EAP=∠E′AO
∴△APE≌△AOE′(ASA),
∴∠OAE′=∠PAE.
在Rt△AEM和Rt△ABN中,
,
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
,
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
(108°-60°)=24°,
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
,
故④错误.
故答案:①.
∠M=∠N ∠AEM=∠ABN=72° AE=AB ∠M=∠N ∠M=∠N ∠M=∠N∠AEM=∠ABN=72° ∠AEM=∠ABN=72° ∠AEM=∠ABN=72°AE=AB AE=AB AE=AB
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
,
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
(108°-60°)=24°,
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
,
故④错误.
故答案:①.
AP=AO AM=AN AP=AO AP=AO AP=AOAM=AN AM=AN AM=AN
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
(108°-60°)=24°,
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
,
故④错误.
故答案:①.
1 2 1 1 12 2 2(108°-60°)=24°,
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
,
故④错误.
故答案:①.
180° n+3 180° 180° 180°n+3 n+3 n+3,
故④错误.
故答案:①.
∴AB=AD,∠D=∠B=90°,
由旋转的性质得,AD=AD′,∠D=∠D′=90°,
∴AB=AD′,
在Rt△ABO与Rt△AD′O中,
|
∴Rt△ABO≌Rt△AD′O,
故①正确;
②如图2,

作AM⊥DE于M,作AN⊥CB于N.
∵五边形ABCDE是正五边形,
由旋转知:AE=AE',∠E=∠E'=108°,∠EAE'=∠OAP=60°,
∴∠EAP=∠E'AO,
在△APE与△AOE'中,
|
∴△APE≌△AOE′(ASA),
∴∠OAE′=∠PAE.
在Rt△AEM和Rt△ABN中,
|
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
|
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
| 1 |
| 2 |
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
| 180° |
| n+3 |
故④错误.
故答案:①.
|
| AB=AD′ |
| AO=AO |
| AB=AD′ |
| AO=AO |
| AB=AD′ |
| AO=AO |
| AB=AD′ |
| AO=AO |
∴Rt△ABO≌Rt△AD′O,
故①正确;
②如图2,

作AM⊥DE于M,作AN⊥CB于N.
∵五边形ABCDE是正五边形,
由旋转知:AE=AE',∠E=∠E'=108°,∠EAE'=∠OAP=60°,
∴∠EAP=∠E'AO,
在△APE与△AOE'中,
|
∴△APE≌△AOE′(ASA),
∴∠OAE′=∠PAE.
在Rt△AEM和Rt△ABN中,
|
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
|
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
| 1 |
| 2 |
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
| 180° |
| n+3 |
故④错误.
故答案:①.
|
| ∠E=∠E′=108° |
| AE=AE′ |
| ∠EAP=∠E′AO |
| ∠E=∠E′=108° |
| AE=AE′ |
| ∠EAP=∠E′AO |
| ∠E=∠E′=108° |
| AE=AE′ |
| ∠EAP=∠E′AO |
| ∠E=∠E′=108° |
| AE=AE′ |
| ∠EAP=∠E′AO |
∴△APE≌△AOE′(ASA),
∴∠OAE′=∠PAE.
在Rt△AEM和Rt△ABN中,
|
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
|
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
| 1 |
| 2 |
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
| 180° |
| n+3 |
故④错误.
故答案:①.
|
| ∠M=∠N |
| ∠AEM=∠ABN=72° |
| AE=AB |
| ∠M=∠N |
| ∠AEM=∠ABN=72° |
| AE=AB |
| ∠M=∠N |
| ∠AEM=∠ABN=72° |
| AE=AB |
| ∠M=∠N |
| ∠AEM=∠ABN=72° |
| AE=AB |
∴Rt△AEM≌Rt△ABN (AAS),
∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,
|
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
| 1 |
| 2 |
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
| 180° |
| n+3 |
故④错误.
故答案:①.
|
| AP=AO |
| AM=AN |
| AP=AO |
| AM=AN |
| AP=AO |
| AM=AN |
| AP=AO |
| AM=AN |
∴Rt△APM≌Rt△AON (HL).
∴∠PAM=∠OAN,
∴∠PAE=∠OAB,
∴∠OAE'=∠OAB=
| 1 |
| 2 |
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
| 180° |
| n+3 |
故④错误.
故答案:①.
| 1 |
| 2 |
故②错误;
③如图3,

∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,
∴∠F=F′=120°,
由旋转得,AF=AF′,EF=E′F′,
∴△APF≌△AE′F′,
∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形,
故③错误.
④由图1中的多边形是四边形,图2中的多边形五边形,图3中的多边形是六边形,
∴图n中的多边形是正(n+3)边形,
同②的方法得,∠OAB=[(n+3-2)×180°÷(n+3)-60°]÷2=60°-
| 180° |
| n+3 |
故④错误.
故答案:①.
| 180° |
| n+3 |
故④错误.
故答案:①.
看了 如图,在正n边形(n为整数,...的网友还看了以下:
四角星的对称轴的相较于点O,绕点O旋转四角星,分别得到什么形状,旋转90°旋转180°旋转360° 2020-04-26 …
如图,点O是边长为2的正方形ABCD的对称中心,过点O作OM⊥ON,分别交正方形边于M,N,G,H 2020-05-17 …
如图①,已知点O为菱形ABCD的对称中心,∠A=60°,将等边△OEF的顶点放在点O处,OE,OF 2020-06-12 …
设曲线y=ax^2(x>=0,常数a>0)与曲线y=1-x^2交于点A,过坐标原点O和点A的直线设 2020-06-14 …
对于点O、M,点M沿MO的方向运动到O左转弯继续运动到N,使OM=ON,且OM⊥ON,这一过程称为 2020-06-19 …
如图,点O是平行四边形ABCD的对称中心,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F. 2020-06-19 …
如下图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为 2020-06-20 …
如下图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为 2020-06-30 …
已知在直角坐标系中,点A的坐标是(-3,1),将线段OA绕着点O顺时针旋转90°得到OB.(1)求 2020-07-24 …
已知,点O为矩形BHCM的对称中心,将一直角的顶点放在点O处,绕点O旋转,直角两边分别交直线BH、H 2020-11-01 …