早教吧作业答案频道 -->数学-->
如图,反比例函数y=kx的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=kx在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-2时,求△OCD的面
题目详情
如图,反比例函数y=
的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=
在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
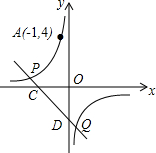
(1)求k的值;
(2)当b=-2时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.
| k |
| x |
| k |
| x |

(1)求k的值;
(2)当b=-2时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.
▼优质解答
答案和解析
(1)∵反比例函数y=
的图象经过点A(-1,4),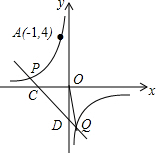
∴k=-1×4=-4;
(2)当b=-2时,直线解析式为y=-x-2,
∵y=0时,-x-2=0,解得x=-2,
∴C(-2,0),
∵当x=0时,y=-x-2=-2,
∴D(0,-2),
∴S△OCD=
×2×2=2;
(3)存在.
当y=0时,-x+b=0,解得x=b,则C(b,0),
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等,
而Q点在第四象限,
∴Q的横坐标为-b,
当x=-b时,y=-x+b=2b,则Q(-b,2b),
∵点Q在反比例函数y=-
的图象上,
∴-b•2b=-4,解得b=-
或b=
(舍去),
∴b的值为-
.
| k |
| x |

∴k=-1×4=-4;
(2)当b=-2时,直线解析式为y=-x-2,
∵y=0时,-x-2=0,解得x=-2,
∴C(-2,0),
∵当x=0时,y=-x-2=-2,
∴D(0,-2),
∴S△OCD=
| 1 |
| 2 |
(3)存在.
当y=0时,-x+b=0,解得x=b,则C(b,0),
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等,
而Q点在第四象限,
∴Q的横坐标为-b,
当x=-b时,y=-x+b=2b,则Q(-b,2b),
∵点Q在反比例函数y=-
| 4 |
| x |
∴-b•2b=-4,解得b=-
| 2 |
| 2 |
∴b的值为-
| 2 |
看了 如图,反比例函数y=kx的图...的网友还看了以下:
若抛物线y=ax^2+bx+c的图像经过A(1,3),B(2,5),C(-2,-3)三点,··1) 2020-05-16 …
质点在x轴简谐震动.选质点向右运动过A点时作计时起点t=0,经2秒后质点运动到B点,再经过2秒后质 2020-07-15 …
一个质点在平衡位置O点附近振动.如果不计阻力,可将这个振动看作周期运动.他离开O点向左运动,4S后 2020-07-20 …
一个质点在O点附近做简协振动,它离开O点向M点运动,经过0.5s第一次到达M点,又经过0.2s第二 2020-07-21 …
一弹簧振子做机械振动,若从平衡位置开始计时,经过0.3秒时振子第一次经过P点,又经过了0.2秒,振 2020-07-22 …
一个质点在平衡位置O点附近做简谐运动,若从O点开始计时,经过3s质点第一次经过M点(如图所示);再 2020-07-22 …
一个质点在平衡位置O点附近做简谐运动,某时刻过O点后经3s时间第一次经过M点,再经2s第二次经过M 2020-07-31 …
两个质点做振幅、周期均相同的简谐振动,第一个质点的振动方程为x1=Acos(ωt+φ).当第一个质 2020-07-31 …
一个质点在平衡位置O点附近做机械振动.若从O点开始计时,经过3s质点第一次经过M点(如图所示);再继 2020-11-27 …
一个质点在平衡位置o点附近做简谐运动,当质点从o点向某一侧运动时,经过3s第一次经过某点M,再向前运 2020-12-15 …