早教吧作业答案频道 -->数学-->
自主学习,请阅读下列解题过程.解一元二次不等式:x2-5x>0.设x2-5x=0,解得:x1=0,x2=5,则抛物线y=x2-5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2-5x的大致图象(如图所示
题目详情
自主学习,请阅读下列解题过程.
解一元二次不等式:x2-5x>0.
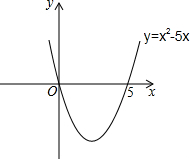
设x2-5x=0,解得:x1=0,x2=5,则抛物线y=x2-5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2-5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2-5x>0,所以,一元二次不等式x2-5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的___和___.(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2-5x<0的解集为___.
(3)用类似的方法解一元二次不等式:x2-2x-3>0.
解一元二次不等式:x2-5x>0.
设x2-5x=0,解得:x1=0,x2=5,则抛物线y=x2-5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2-5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2-5x>0,所以,一元二次不等式x2-5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:

(1)上述解题过程中,渗透了下列数学思想中的___和___.(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2-5x<0的解集为___.
(3)用类似的方法解一元二次不等式:x2-2x-3>0.
▼优质解答
答案和解析
(1)上述解题过程中,渗透了下列数学思想中的①和③;
故答案为:①,③;
(2)由图象可知:当0此时y<0,即x2-5x<0,
∴一元二次不等式x2-5x<0的解集为:0故答案为:0
(3)设x2-2x-3=0,
解得:x1=3,x2=-1,
∴抛物线y=x2-2x-3与x轴的交点坐标为(3,0)和(-1,0).
画出二次函数y=x2-2x-3的大致图象(如图所示),
由图象可知:当x<-1,或x>3时函数图象位于x轴上方,
此时y>0,即x2-2x-3>0,
∴一元二次不等式x2-2x-3>0的解集为:x<-1,或x>3.
故答案为:①,③;
(2)由图象可知:当0
∴一元二次不等式x2-5x<0的解集为:0
(3)设x2-2x-3=0,
解得:x1=3,x2=-1,
∴抛物线y=x2-2x-3与x轴的交点坐标为(3,0)和(-1,0).
画出二次函数y=x2-2x-3的大致图象(如图所示),
由图象可知:当x<-1,或x>3时函数图象位于x轴上方,
此时y>0,即x2-2x-3>0,
∴一元二次不等式x2-2x-3>0的解集为:x<-1,或x>3.
看了 自主学习,请阅读下列解题过程...的网友还看了以下:
大学数学求两个直交圆柱面x^2+y^2=r^2和x^2+z^2=r^2所围立体表面积,答案是16r 2020-05-16 …
二年级一班有45人,她们和9位老师一起去湖滨公园划船(大船限坐8人,小船限坐6人)如果都坐小船,要 2020-05-16 …
英语翻译在我的理解里,邓迪大学(The University of Dundee)是英国一所拥有相 2020-05-17 …
英语翻译在我们班,一共有50名学生.大概有15名同学,是坐公共汽车来上学的.另外有15名同学是坐地 2020-05-23 …
有两条直线,y1=ax+by2=cx+5c学生甲解除他们的交点坐标为(3,-2)学生乙因把C抄错了 2020-06-06 …
一道初中数学坐标几何题点A坐标为(1,3),点B坐标为(4,-1),P点为X轴上一点,当点P坐标为 2020-06-14 …
有两条直线y1=ax+b,y2=cx+5c学生甲解出它们的交点坐标为(2,-3)学生乙因把c抄错而 2020-06-24 …
英语翻译在我的理解里,邓迪大学(TheUniversityofDundee)是英国一所拥有相当悠久 2020-07-12 …
同学们乘坐大、中型两种车去春游,大型车每辆坐65人,中型车每辆坐26人.现有学生现有学生与教师33 2020-07-19 …
有机化学中用杂化来解释键长键能的问题小弟大学有机化学坐的飞机不好意思啊1.用杂化理论解释为什么甲烷乙 2020-11-29 …