早教吧作业答案频道 -->数学-->
如图,已知二次函数y=ax2+bx+c的图象顶点在x轴上,且OA=1,与一次函数y=-x-1的图象交于y轴上一点B和另一交点C.(1)求抛物线的解析式;(2)点D为线段BC上一点,过点D作DE⊥x轴,垂足为E,
题目详情
如图,已知二次函数y=ax2+bx+c的图象顶点在x轴上,且OA=1,与一次函数y=-x-1的图象交于y轴上一点B和另一交点C.
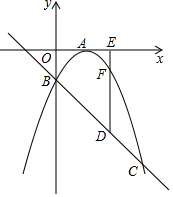
(1)求抛物线的解析式;
(2)点D为线段BC上一点,过点D作DE⊥x轴,垂足为E,交抛物线于点F,请求出线段DF的最大值.

(1)求抛物线的解析式;
(2)点D为线段BC上一点,过点D作DE⊥x轴,垂足为E,交抛物线于点F,请求出线段DF的最大值.
▼优质解答
答案和解析
(1)∵OA=1,
∴抛物线的顶点A的坐标为(1,0),
设抛物线解析式为y=a(x-1)2,
在直线y=-x-1中,当x=0时,y=-1,
则点B(0,-1),代入得:a=-1,
∴抛物线解析式为y=-(x-1)2=-x2+2x-1.
(2)由
,解得
或
,
即点B(0,-1)、点C(3,-4),
∴0<x<3,
令DF=W,
则W=-(-x-1)-(-x2+2x-1)=x2-x+2=(x-
)2+
,
∴当x=
时,W最大值=
,
即线段DF的最大值为
.
∴抛物线的顶点A的坐标为(1,0),
设抛物线解析式为y=a(x-1)2,
在直线y=-x-1中,当x=0时,y=-1,
则点B(0,-1),代入得:a=-1,
∴抛物线解析式为y=-(x-1)2=-x2+2x-1.
(2)由
|
|
|
即点B(0,-1)、点C(3,-4),
∴0<x<3,
令DF=W,
则W=-(-x-1)-(-x2+2x-1)=x2-x+2=(x-
| 1 |
| 4 |
| 7 |
| 4 |
∴当x=
| 1 |
| 4 |
| 7 |
| 4 |
即线段DF的最大值为
| 7 |
| 4 |
看了 如图,已知二次函数y=ax2...的网友还看了以下:
圆内两弦相交,一弦长为8cm,且被交点平分,另一弦被交点分成的两段的比是1:4,那么另一弦长是() 2020-04-26 …
如图,在平行四边形ABCD中,点E、F、G、H分别为四边上的中点,且EG交FH与点N,请指出图中的 2020-05-13 …
CAD:三条直线,其中a,b两条直线相交且角度知道但长度不知道;另一条直线c知道长度和角度,怎么确 2020-05-13 …
已知抛物线的解析式为y=-x2+2mx+4-m2.(1)求证:不论m取何值,此抛物线与x轴必有两个 2020-05-16 …
九上数学题圆如图三角形ABC内接于圆o且BC是圆0的直径如图,三角形ABC内接于圆o,且BC是圆o 2020-06-03 …
求抛物线与直线的交点已知抛物线y=ax^2-2ax与直线l:y=ax(a大于0)交点除原点外,另交 2020-06-05 …
ABCD空间四边形 E,F是AB,BC中点 点G,H在CD,AD上 DH=1/3AD,DG=1/3 2020-06-27 …
a为何值时,抛物线y^2=x+a和x^2=y+a有四个交点?证明当这两条抛物线有四个交点时,这四个 2020-07-21 …
如图,在平行四边形ABCD中,M是BC边上一点,且AM交与BD与N,AM比NM=4比11.试说明三 2020-08-01 …
如图,在坐标系中xOy中:点A在直线y=根号3x的图像上,其横坐标为1,过A点的直线平行于x轴,交y 2021-01-10 …