已知某海滨浴场的海浪高度（单位：米）是时间（单位：小时，0≤t≤24）的函数，记作y=f（t），如表是某日各时的浪高数据：t（时）03691215182124y（米）1.51.00.51.01.51.00.51.01.5

Question

已知某海滨浴场的海浪高度（单位：米）是时间（单位：小时，0≤t≤24）的函数，记作y=f（t），如表是某日各时的浪高数据：

t（时）	0	3	6	9	12	15	18	21	24
y（米）	1.5	1.0	0.5	1.0	1.5	1.0	0.5	1.0	1.5

（Ⅰ）在如图的网格中描出所给的点；
（Ⅱ）观察图，从y=at+b，y=at²+bt+c，y=Acos（ωx+p）中选择一个合适的函数模型，并求出该拟合模型的解析式；
（Ⅲ）依据规定，当海浪高度高于1.25米时蔡对冲浪爱好者开放，请依据（Ⅱ）的结论判断一天内的8：00到20：00之间有多长时间可供冲浪爱好者进行活动．

Answer 1

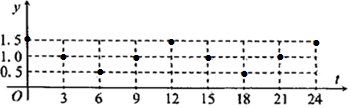
（Ⅰ）由表中数据描点如图：
；
（Ⅱ）由图可知，应选择的函数模型为：y=Acos（ωt+φ）+b．
不妨设A>0，ω>0，
则A=(1.5-0.5)/(2)=0.5，b=(1.5+0.5)/(2)=1，(2π)/(ω)=12，ω=(π)/(6)．
∴y=0.5cos（(π)/(6)t+φ）+1，
又当x=0时，y=1.5，
∴0.5cosφ+1=1.5，得cosφ=1，则φ=2kπ，k∈Z．
∴y=0.5cos（(π)/(6)t+2kπ）+1=0.5cos(π)/(6)t+1，（0≤t≤24）；
（Ⅲ）由0.5cos(π)/(6)t+1>1.25，得cos(π)/(6)t>(1)/(2)，
∴2kπ-(π)/(3)<(π)/(6)t<2kπ+(π)/(3)，即12k-2<t<12k+2，k∈Z．
又8≤t≤20，∴10<t<14．
故一天内的8：00到20：00之间有4个小时可供冲浪爱好者进行活动．