如图，E、F、G、H分别是空间四边形ABCD各边上的点，且有AE∶EB=AH∶HD=mCF∶FB=CG∶GD=n.(1)证明E、F、G、H四点共面；(2)m、n满足什么条件时，四边形EFGH是平行四边形？(3)在(2)的条

Question

如图，E、F、G、H分别是空间四边形ABCD各边上的点，且有AE∶EB=AH∶HD=m CF∶FB=CG∶GD=n.

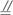
(1)证明E、F、G、H四点共面；

(2)m、n满足什么条件时，四边形EFGH是平行四边形？

(3)在(2)的条件下，若AC⊥BD，试证明EG=FH.

Answer 1

（1）证明:∵AE∶EB=AH∶HD，

∴EH∥BD.

∵CF∶FB=CG∶GD，

∴FG∥BD.∴EH∥FG.

∴E、F、G、H四点共面.

（2）解析:

当且仅当EH FG时，四边形EFGH为平行四边形.

∵

∴EH= BD.

同理 FG= BD.由EH=FG 得m=n.

故当m=n时，四边形EFGH为平行四边形.

（3）证明:当m=n时，AE∶EB=CF∶FB

∴EF∥AC.

又∵AC⊥BD，

∴∠FEH是AC与BD所成的角.

∴∠FEH=90°，从而四边形EFGH为矩形.

∴EG=FH.

小结:空间四边形是立体几何的一个基本图形，它各边中点连线构成平行四边形；当两对角线相等时该平行四边形为菱形；当两对角线互相垂直时，该平行四边形为矩形；当两对角线相等且互相垂直时 该平行四边形为正方形.