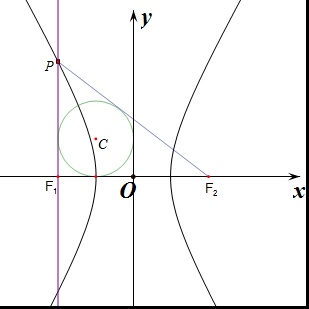
设双曲线C：x2a2-y2b2=1（a>0，b>0）左，右焦点为F1，F2，P是双曲线C上的一点，PF1与x轴垂直，△PF1F2的内切圆方程为（x+1）2+（y-1）2=1，则双曲线方程为（）A.x22-y23=1B.x2-y22=1C.x22-y2=1D.

Question

设双曲线C：

(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）左，右焦点为F₁，F₂，P是双曲线C上的一点，PF₁与x轴垂直，△PF₁F₂的内切圆方程为（x+1）²+（y-1）²=1，则双曲线方程为（　　）

A.

(x2)/(2)-(y2)/(3)=1

B. x2-

(y2)/(2)=1

C.

(x2)/(2)-y2=1

D. x2-

(y2)/(3)=1

Answer 1

，△PF₁F₂的内切圆方程为（x+1）²+（y-1）²=1，圆心C（-1，1），半径为r=1，
∴丨OF₁丨=2r=2，
P（-2，(b2)/(a)），
∴丨PF₁丨=(b2)/(a)，由双曲线的定义可知：丨PF₂丨=2a+(b2)/(a)，丨F₁F₂丨=2c=4，
由三角形的内切圆的半径r=(丨PF1丨+丨F1F2丨-丨PF2丨)/(2)=2-a=1，
则a=1，
由b²=c²-a²=3
∴双曲线方程为：x2-(y2)/(3)=1，
故选D．