早教吧作业答案频道 -->数学-->
如图,ABCD是一张矩形纸片,AD=BC=2,AB=CD=10,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.(1)若∠1=70°,求∠MKN的度数;(2)当折痕MN与对角线
题目详情
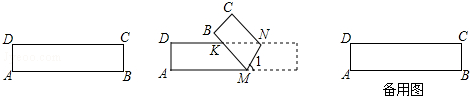
如图,ABCD是一张矩形纸片,AD=BC=2,AB=CD=10,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)若∠1=70°,求∠MKN的度数;
(2)当折痕MN与对角线AC重合时,试求△MNK的面积;
(3)△MNK的面积能否小于2?若能,求出此时∠1的度数;若不能,试说明理由.
(1)若∠1=70°,求∠MKN的度数;
(2)当折痕MN与对角线AC重合时,试求△MNK的面积;
(3)△MNK的面积能否小于2?若能,求出此时∠1的度数;若不能,试说明理由.

▼优质解答
答案和解析
(1)∵四边形ABCD是矩形,
∴AM∥DN,
∴∠KNM=∠1,
∵∠KMN=∠1,
∴∠KNM=∠KMN,
∵∠1=70°,
∴∠KNM=∠KMN=70°,
∴∠MKN=40°;
(2)如图1,
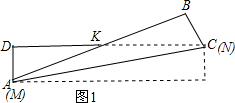
折痕即为AC,此时△AKC为等腰三角形,
设MK=AK=CK=x,则DK=10-x,
在Rt△ADK中,根据勾股定理得:AD2+DK2=AK2,
即22+(10-x)2=x2,
解得:x=2.6,
∴MK=AK=CK=5.2,S△MNK=S△ACK=
×2×5.2=5.2,
∴△MNK的面积的为5.2;
(3)不能,如图2,
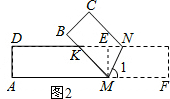
理由如下:过M点作AE⊥DN,垂足为点E,则ME=AD=2,
由(1)知,∠KNM=∠KMN,
∴MK=NK,
又∵MK≥ME,ME=AD=2,
∴MK≥2,
又∵S△MNK=
NK•ME≥2,
即△MNK面积的最小值为2,
∴△MNK的面积不能小于2.
∴AM∥DN,
∴∠KNM=∠1,
∵∠KMN=∠1,
∴∠KNM=∠KMN,
∵∠1=70°,
∴∠KNM=∠KMN=70°,
∴∠MKN=40°;
(2)如图1,

折痕即为AC,此时△AKC为等腰三角形,
设MK=AK=CK=x,则DK=10-x,
在Rt△ADK中,根据勾股定理得:AD2+DK2=AK2,
即22+(10-x)2=x2,
解得:x=2.6,
∴MK=AK=CK=5.2,S△MNK=S△ACK=
| 1 |
| 2 |
∴△MNK的面积的为5.2;
(3)不能,如图2,

理由如下:过M点作AE⊥DN,垂足为点E,则ME=AD=2,
由(1)知,∠KNM=∠KMN,
∴MK=NK,
又∵MK≥ME,ME=AD=2,
∴MK≥2,
又∵S△MNK=
| 1 |
| 2 |
即△MNK面积的最小值为2,
∴△MNK的面积不能小于2.
看了如图,ABCD是一张矩形纸片,...的网友还看了以下:
从原点出发的某质点M按向量移动,是怎样移动的?是否与向量的模长有关?如题:从原点出发的某质点M,按 2020-05-20 …
(2012•海淀区二模)已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为 2020-06-12 …
已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.(1)求过M点的圆的切 2020-07-12 …
已知点H(-3,0),点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且HP•PM=0,又PM 2020-07-15 …
如图,在平面直角坐标系中,A点的坐标是(3,4),AB⊥x轴于点B,反比例函数y=kx的图象中的一 2020-07-24 …
1.如图所示,已知线段AB=20cm,点M是线段AB中点,点C是线段AB延长线上的点,AC=3BC 2020-07-25 …
如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣 2020-07-31 …
设x在数轴上对应点M,若将M点向右移动3个单位长度后再向左移动4个单位长度得到N点,则M点对应的有理 2020-11-18 …
两列水波发生干涉,在某时刻,M点是波峰与波峰相遇处,N点是波谷与波谷相遇处,P点的位移为零,Q点是波 2020-12-15 …
两列水波发生干涉,在某时刻,M点是波峰与波峰相遇处,N点是波谷与波谷相遇处,P点的位移为零,Q点是波 2020-12-27 …