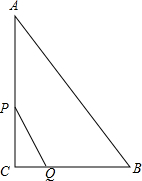
如图，在△ABC中，∠C=90°，AC=80cm，BC=60cm，动点P在线段CA上从C点出发沿CA方向以12cm/s的速度向终点A运动，动点Q在线段CB上从C点出发沿CB方向以5cm/s的速度向终点B运动，如果P，Q两点同时从C点

Question

如图，在△ABC中，∠C=90°，AC=80cm，BC=60cm，动点P在线段CA上从C点出发沿CA方向以12cm/s的速度向终点A运动，动点Q在线段CB上从C点出发沿CB方向以5cm/s的速度向终点B运动，如果P，Q两点同时从C点出发开始运动，当一点到达终点时，另一点也停止运动，设运动t秒（0<t<(20)/(3)）时，四边形APQB的周长为y（cm），请解决下列问题：

（1）试用含t的代数式分别表示线段AP，QB，PQ的长度．
（2）写出四边形APQB的周长y（cm）与运动时间t（秒）之间的函数关系式．
（3）是否存在某一时刻t，使四边形APQB的周长与△ABC的周长比为11：12？若存在请求出t的值，若不存在请说明理由．

Answer 1

（1）∵AC=80cm，BC=60cm，
∴CP=12t，CQ=5t，
∴AP=80-12t，BQ=60-5t，
在Rt△PCQ中，PQ=√(CP2+CQ2)=13t，
（2）在Rt△ABC中，AC=80，BC=60，
∴AB=100，
由（1）知，PQ=13t，AP=80-12t，BQ=60-5t，
∴四边形APQB的周长y=AP+AB+BQ+PQ=80-12t+100+60-5t+13t=240-4t（0<t<(20)/(3)）；
（3）由（2）知，AB=100，
∵AB=80，BC=60，
∴△ABC的周长=AB+AC+BC=100+80+60=240，
∵四边形APQB的周长与△ABC的周长比为11：12，
∴四边形APQB的周长为(11)/(12)×240=220，
由（2）知，四边形APQB的周长y=240-4t
∴240-4t=220，
∴t=5，
∴存在时间t=5秒时，四边形APQB的周长与△ABC的周长比为11：12．