早教吧作业答案频道 -->数学-->
如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.(1)判断AF与DF的数量关系,并说明理由.(2)只用无刻度的直尺画出△ADE的
题目详情
如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.
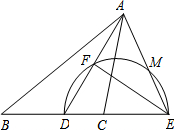
(1)判断AF与DF的数量关系,并说明理由.
(2)只用无刻度的直尺画出△ADE的边DE上的高AH(不要求写作法,保留作图痕迹).
(3)若EF=8,DF=6,求DH的长.

(1)判断AF与DF的数量关系,并说明理由.
(2)只用无刻度的直尺画出△ADE的边DE上的高AH(不要求写作法,保留作图痕迹).
(3)若EF=8,DF=6,求DH的长.
▼优质解答
答案和解析
(1)AF=DF,
理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠B=∠CAE,
∴∠BAD+∠B=∠CAD+∠CAE.
即∠ADE=∠DAE,
∴AE=DE,
∵DE是直径,
∴EF⊥AD,
∴AF=DF;
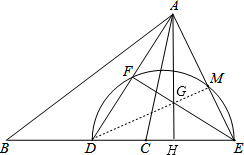 (2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(3)在△EFD中,EF=8,DF=6,由勾股定理得,DE=AE=10,
∵AH是DE边上的高,
∴∠AHD=90°,
∵∠EFD=90°,
∴∠AHD=∠EFD,
∵∠ADH=∠EDF,
∴△ADH∽△EDF,
∴
=
,
∴
=
,
解得DH=
.
理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠B=∠CAE,
∴∠BAD+∠B=∠CAD+∠CAE.
即∠ADE=∠DAE,
∴AE=DE,
∵DE是直径,
∴EF⊥AD,
∴AF=DF;
 (2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.(3)在△EFD中,EF=8,DF=6,由勾股定理得,DE=AE=10,
∵AH是DE边上的高,
∴∠AHD=90°,
∵∠EFD=90°,
∴∠AHD=∠EFD,
∵∠ADH=∠EDF,
∴△ADH∽△EDF,
∴
| DH |
| DF |
| AD |
| DE |
∴
| DH |
| 6 |
| 12 |
| 10 |
解得DH=
| 36 |
| 5 |
看了如图,在△ABC中,AD为∠B...的网友还看了以下:
8、(2011绵阳)已知抛物线y=x2-2x+m-1与x轴只有一个交点,且与y轴交于A点,如图,设 2020-05-16 …
二次函数y=ax^2+bx+c(a不等于0)图像的顶点为D,其图像与x轴的交点A、B的横坐标是-1 2020-05-16 …
对既属于大额交易又属于可疑交易的交易,金融机构应当()A.合并提交报告B.只提交可疑交易报告C.分 2020-05-27 …
Ax+By+C=0直线与两坐标轴都相交A不等于0且B不等于0,C为任意实数那如果C=0,不是这条直 2020-07-09 …
关于交流电的下列说法正确的是[]A.在一个周期内交流电的方向只改变一次B.交流电器设备上标出的电压 2020-07-19 …
已知抛物线y=x2-2x+m-1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B。(1) 2020-07-21 …
(2011•绵阳)已知抛物线y=x2-2x+m-1与x轴只有一个交点,且与y轴交于A点,如图,设它的 2020-11-01 …
据调查,一个人事业上的成功,只有15%靠的是专业技术,另外的85%要靠沟通技巧。由此可见()A.只要 2021-01-05 …
点O在∠APB的平分线上,圆O与PA相切与点C,求证PB与圆O相切点A、P、B均是圆O的点,连接AP 2021-01-11 …
价值规律告诉我们,商品交换以价值量为基础,实行等价交换.这里的“等价交换”A.只存在于交换的平均数中 2021-01-13 …