早教吧作业答案频道 -->数学-->
如图1将矩形ABCD折叠,使得顶点B落在CD边上的P点处,已知折痕与边BC交于点O,连结AP、OP、OA.(1)求证:△OCP∽△PDA;(2)如图2,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P
题目详情
如图1将矩形ABCD折叠,使得顶点B落在CD边上的P点处,已知折痕与边BC交于点O,连结AP、OP、OA.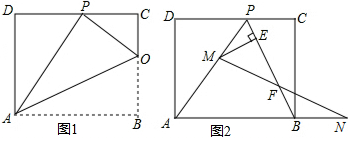
(1)求证:△OCP∽△PDA;
(2)如图2,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.探究:当点M、N在移动过程中,线段EF与线段PB有何数量关系?并说明理由.

(1)求证:△OCP∽△PDA;
(2)如图2,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.探究:当点M、N在移动过程中,线段EF与线段PB有何数量关系?并说明理由.
▼优质解答
答案和解析
(1)如图1,∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B,
∴∠APO=90°.
∴∠APD=90°-∠CPO=∠POC,
∴△OCP∽△PDA;
(2)作MQ∥AN,交PB于点Q,如图2,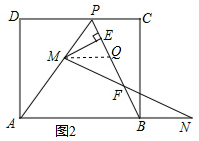
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP,∠ABP=∠MQP,
∴∠APB=∠MQP,
∴MP=MQ,
∵MP=MQ,ME⊥PQ,
∴PE=EQ=
PQ,
∵BN=PM,MP=MQ,
∴BN=QM,
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
,
∴△MFQ≌△NFB,
∴QF=BF,
∴QF=
QB,
∴EF=EQ+QF=
PQ+
QB=
PB.
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B,
∴∠APO=90°.
∴∠APD=90°-∠CPO=∠POC,
∴△OCP∽△PDA;
(2)作MQ∥AN,交PB于点Q,如图2,

∵AP=AB,MQ∥AN,
∴∠APB=∠ABP,∠ABP=∠MQP,
∴∠APB=∠MQP,
∴MP=MQ,
∵MP=MQ,ME⊥PQ,
∴PE=EQ=
| 1 |
| 2 |
∵BN=PM,MP=MQ,
∴BN=QM,
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
|
∴△MFQ≌△NFB,
∴QF=BF,
∴QF=
| 1 |
| 2 |
∴EF=EQ+QF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
看了如图1将矩形ABCD折叠,使得...的网友还看了以下:
已知函数f(X)=x^(-1/2p^2+p+3/2)(p属于Z)在(0,+无穷)上是增函数,且在其 2020-05-13 …
解方程.并在括号里指明步骤的依据 三分之2x+1-六分之10x+1=1 _____,得2(2x+1 2020-05-16 …
甲乙两棋友下棋,每盘比赛中,甲取胜的概率为0.5,乙取胜的概率为0.4,两人平局的概率为0.1,他 2020-06-04 …
甲乙两棋友下棋.每盘比赛中,甲取胜的概率为0.5,乙取胜的概率为0.4,两人平局的概率为0.1.他 2020-06-04 …
一个分数的分母减去3得3分之2,将它的分母加上1,侧得2分之1,求这个分数是多少 2020-06-20 …
解不等式|x-2|≤1时,我们可以采用下面的解法:①.当x-2≥0时,|x-2|=x-2∴原不等式 2020-07-03 …
帮忙填上合适的词语列如:疼的泪眼汪汪1.累得2.坐得3.吃得4.睡得5.得6.得7.得要仿照列子的 2020-07-10 …
数学排列组合有6件不同的礼品按下面的分法有多少种分法1.分给甲乙丙三人每人各得2件2.分给三人,甲得 2020-12-09 …
(1)(5分)(2015·宁夏银川一中一模)下列说法正确的是。(填正确答案标号选对1个得2分选对2个 2020-12-18 …
某种比赛的规则是5局3胜制,甲,乙两人在比赛中获胜的概率分别为2/3和1/3.若胜1局得2分,负1局 2021-01-14 …