早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.(1)如图1,若α=60°,点P与点M重合,则∠BDA=
题目详情
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
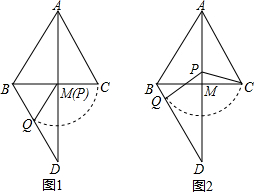
(1)如图1,若α=60°,点P与点M重合,则∠BDA=___;
(2)如图2,点P不与点A、点M重合,则∠BDA=___.(用含α的式子表示)

(1)如图1,若α=60°,点P与点M重合,则∠BDA=___;
(2)如图2,点P不与点A、点M重合,则∠BDA=___.(用含α的式子表示)
▼优质解答
答案和解析
(1)∵AB=AC,M是BC的中点,
∴AM⊥BC,
∴∠BMD=90°,
∵∠CMQ=2α=120°,
∴∠BMP=60°,
∵BM=MC=MQ,
∴∠MBQ=60°,
∴∠BDA=90°-60°=30°,
故答案为:30°;
(2)如图,连接PB,CD,
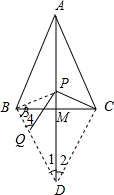
∵AC=AB,M是BC的中点,
∴AM⊥BC,
即AD为BC的垂直平分线,
∴BD=CD,BP=PC,PD=PD,
在△BPD与△CPD中,
,
∴△BPD≌△CPD(SSS),
∴∠CDA=∠BDA,∠PBD=∠PCD,
又∵PQ=PC,
∴PQ=PB,∠BDC=2∠1,∠4=∠PBQ=∠PCD,
∴∠PCD+∠PQD=∠4+∠PQD=180°,
∴∠CPQ+∠BDC=360°-(∠PCD+∠PQD)=180°,
∴∠BDA=180°-∠CPQ=180°-2α,
∴2∠BDA=180°-2α,
∴∠BDA=90°-α.
故答案为:90°-α.
∴AM⊥BC,
∴∠BMD=90°,
∵∠CMQ=2α=120°,
∴∠BMP=60°,
∵BM=MC=MQ,
∴∠MBQ=60°,
∴∠BDA=90°-60°=30°,
故答案为:30°;
(2)如图,连接PB,CD,

∵AC=AB,M是BC的中点,
∴AM⊥BC,
即AD为BC的垂直平分线,
∴BD=CD,BP=PC,PD=PD,
在△BPD与△CPD中,
|
∴△BPD≌△CPD(SSS),
∴∠CDA=∠BDA,∠PBD=∠PCD,
又∵PQ=PC,
∴PQ=PB,∠BDC=2∠1,∠4=∠PBQ=∠PCD,
∴∠PCD+∠PQD=∠4+∠PQD=180°,
∴∠CPQ+∠BDC=360°-(∠PCD+∠PQD)=180°,
∴∠BDA=180°-∠CPQ=180°-2α,
∴2∠BDA=180°-2α,
∴∠BDA=90°-α.
故答案为:90°-α.
看了在△ABC中,AB=AC,∠A...的网友还看了以下:
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E交BC于F,边AB折叠后与BC边 2020-05-17 …
关于圆锥曲线的问题若椭圆的中心为原点,焦点在x轴上,点P是椭圆上的一点,P在x轴上的射影恰为椭圆的 2020-06-04 …
如图,⊙O的直径为AB,⊙O1过点O,且与⊙O内切于点B.C为⊙O上的点,OC与⊙O1交于点D,且 2020-06-16 …
(2012•历下区一模)现有甲、乙、丙、丁、戊五种植物.甲与乙属于同一科,甲与丙属于同一属,甲与丁 2020-06-21 …
始臣起下邳;与上会于留,此天以授陛下授始臣起下邳;与上会于留,此天以授陛下中授的意思 2020-06-25 …
设事件A与B的概率均大于零小于1,且A与B相互独立,则有()A.A与B互不相容B.上横杠A与上横杠 2020-07-08 …
如图,在直角坐标系xOy中,一次函数y=-x+b(b为常数)的图象与x轴、y轴分别相交于点A、B; 2020-08-03 …
如图△ABC内接于圆O且AB=AC,点D在圆上AD⊥AB于点A,AD与BC交于点E,如图,△ABC内 2020-11-03 …
如图所示,质量为M的半球面静止在水平地面上,质量为m的小物块在半球面上处于平衡状态,小物块与一轻弹簧 2020-12-05 …
如图,在△ABC中,AB>AC,内切圆I与边BC切于点D,AD与I的另一个交点为E,I的切线EP与B 2021-01-11 …