判断一条直线是否是圆的切线通常有哪些方法？一般如何选取合适的方法？

Question

判断一条直线是否是圆的切线 通常有哪些方法？一般如何选取合适的方法？

Answer 1

判定切线通常有三种方法:

（1）和圆有唯一一个公共点的直线是圆的切线;

（2）和圆心距离等于半径的直线是圆的切线;

（3）过半径外端且和半径垂直的直线是圆的切线.

“过半径外端 垂直于这条半径的直线是圆的切线”只是把“到圆心距离等于半径的直线是圆的切线”的定理具体化 在使用时要根据题目的具体要求选取合适的方法 如果涉及到数值计算或距离问题 通常利用（2） 如果涉及到线段的位置关系等 通常选取（3）.

{{试题大类：选修4-1；题型：填空题；学期：第二讲直线与圆的位置关系；单元：三圆的切线与性质及判定定理；知识点：简易逻辑；难度：易；其它备注：主观题；分值：4$$已知下列5个命题:

(1)过半径外端的直线是圆的切线;

(2)垂直于半径的直线是圆的切线;

(3)经过半径外端和这条直线垂直的直线是圆的切线;

(4)过直径端点且和这条直径垂直的直线是圆的切线;

    (5)和圆有一个交点的直线是圆的切线.

其中正确的命题序号是          .

@@首先判断这些命题的条件与切线判定定理或定义是否一致.(3)(4)正确.

【例1】{{试题大类：选修4-1；题型：解答题；学期：第二讲直线与圆的位置关系；单元：三圆的切线与性质及判定定理；知识点：圆的方程、直线与圆的位置关系；难度：易；其它备注：主观题；分值：8$$ 如图2-3-2所示 梯形 ABCD 中 AD ∥ BC ∠ C =90° 且 AD + BC = AB AB 为⊙ O 的直径 求证:⊙ O 与 CD 相切.

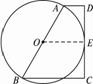
图2-3-2

@@思路解析:欲证⊙ O 与 CD 相切只需证明圆心 O 到直线 CD 的距离等于⊙ O 的半径即可.

证明:过 O 点作 OE ⊥ CD 垂足为 E 

∴ AD ∥ OE ∥ BC .

∵ O 为 AB 的中点 ∴ E 为 CD 的中点.

∴ OE = ( AD + BC ).又∵ AD + BC = AB 

∴ OE = AB =⊙ O 的半径.∴⊙ O 与 CD 相切.