早教吧作业答案频道 -->数学-->
若直角坐标平面内的两个不同点M、N满足条件:①M、N都在函数y=f(x)的图象上;②M、N关于原点对称.则称点对[M,N]为函数y=f(x)的一对“友好点对”.(注:点对[M,N]与[N,M]为
题目详情
若直角坐标平面内的两个不同点M、N满足条件:
①M、N都在函数y=f(x)的图象上;
②M、N关于原点对称.则称点对[M,N]为函数y=f(x)的一对“友好点对”.(注:点对[M,N]与[N,M]为同一“友好点对”),已知函数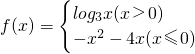 ,此函数的“友好点对”有________.
,此函数的“友好点对”有________.
①M、N都在函数y=f(x)的图象上;
②M、N关于原点对称.则称点对[M,N]为函数y=f(x)的一对“友好点对”.(注:点对[M,N]与[N,M]为同一“友好点对”),已知函数
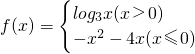 ,此函数的“友好点对”有________.
,此函数的“友好点对”有________.▼优质解答
答案和解析
2个
分析:
根据题意:“友好点对”,可知,欲求f(x)的“友好点对”,只须作出函数y=-x 2 -4x(x≤0)的图象关于原点对称的图象,看它与函数f(x)=log 3 x(x>0)交点个数即可.
根据题意:当x>0时,-x<0,
则f(-x)=-(-x) 2 -4(-x)=-x 2 +4x,
则函数y=-x 2 -4x(x≤0)的图象关于原点对称的函数是y=x 2 -4x(x≥0)
由题意知,作出函数y=x 2 -4x(x≥0)的图象及函数f(x)=log 3 x(x>0)的图象如下图所示
由图可得两个函数图象共有两个交点
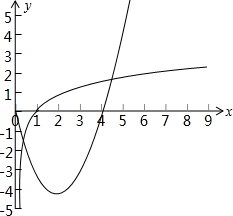
即f(x)的“友好点对”有:2个.
故答案为:2
点评:
本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,解答的关键在于对“友好点对”的正确理解,合理地利用图象法解决.
分析:
根据题意:“友好点对”,可知,欲求f(x)的“友好点对”,只须作出函数y=-x 2 -4x(x≤0)的图象关于原点对称的图象,看它与函数f(x)=log 3 x(x>0)交点个数即可.
根据题意:当x>0时,-x<0,
则f(-x)=-(-x) 2 -4(-x)=-x 2 +4x,
则函数y=-x 2 -4x(x≤0)的图象关于原点对称的函数是y=x 2 -4x(x≥0)
由题意知,作出函数y=x 2 -4x(x≥0)的图象及函数f(x)=log 3 x(x>0)的图象如下图所示
由图可得两个函数图象共有两个交点

即f(x)的“友好点对”有:2个.
故答案为:2
点评:
本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,解答的关键在于对“友好点对”的正确理解,合理地利用图象法解决.
看了若直角坐标平面内的两个不同点M...的网友还看了以下:
在下列格式的括号内填上适当的项1.x-y-z=x+?=x-?2.1-x的平方+xy-y的平方=1- 2020-04-07 …
证明函数f(z)=x^2+2xy-y^2-i(x^2-2xy-y^2)在复平面内处处解析并求其导数 2020-05-20 …
点p(x.,y.)在圆O:x的平方+y的平方=r的平方内,则直线x.x+y.y=r的平方与已知圆O 2020-05-20 …
在平面直角坐标系内,点0为坐标原点,点A,B的坐标分别为(x,y),(x+6,y)~在平面直角坐标 2020-06-02 …
用描述法表示:(1)坐标平面内,不在二,四象限的点的集合;(2)坐标平面内,两坐标轴上的点集.答案 2020-06-14 …
平面直角坐标系内点P(x,y)的横坐标x与纵坐标y满足:-1≤x≤1,-1≤y≤1(1)若x属于Z 2020-06-14 …
在平面直角坐标系中,下列说法错误的是()A.点A(-1,-3)在第四象限内\x05B.若x<0,y 2020-07-30 …
请问:求三元函数f(x,y,z)=x+y+z在曲面S:x平方+y平方=z和平面z=1围成的闭区域D上 2020-11-01 …
教教我!两个小时之内答得好再给50分1、已知y+z分之x=ax+z分之y=bx+y分之z=c求a+1 2020-12-08 …
(2013•松江区一模)定义变换T将平面内的点P(x,y)(x≥0,y≥0)变换到平面内的点Q(x, 2021-01-07 …