定理表述请你根据图1中的直角三角形叙述勾股定理（用文字及符号语言叙述）；尝试证明以图1中的直角三角形为基础，可以构造出以a、b为底，以a+b为高的直角梯形（如图2），请

Question

【定理表述】
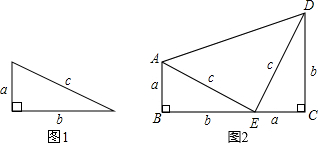
请你根据图1中的直角三角形叙述勾股定理（用文字及符号语言叙述）；
【尝试证明】
以图1中的直角三角形为基础，可以构造出以a、b为底，以a+b为高的直角梯形（如图2），请你利用图2，验证勾股定理；
【知识拓展】
利用图2中的直角梯形，我们可以证明 (a+b)/(c)< √(2)．其证明步骤如下：
∵BC=a+b，AD=___．
又∵在直角梯形ABCD中有BC___AD（填大小关系），即___，
∴ (a+b)/(c)< √(2)．

Answer 1

【定理表述】如果直角三角形的两直角边长分别为a、b，斜边长为c，那么a²+b²=c²．
【尝试证明】
∵Rt△ABE≌Rt△ECD，
∴∠AEB=∠EDC，
又∵∠EDC+∠DEC=90°，
∴∠AEB+∠DEC=90°，
∴∠AED=90°．
∵S_梯形ABCD=S_Rt△ABE+S_Rt△DEC+S_Rt△AED，
∴(1)/(2)（a+b）（a+b）=(1)/(2)ab+(1)/(2)ab+(1)/(2)c²，
整理，得a²+b²=c²．
【知识拓展】
∵AD=√(2)c，BC<AD，
∴a+b<√(2)c，即(a+b)/(c)<√(2)，
故答案为：√(2)c，<，a+b<√(2)c