(1)证明f(x)是奇函数,并求其单调区间;(2)分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并由此概括一个涉及函数f(x)、g(x)的对所有非零实数x都成立的等式,
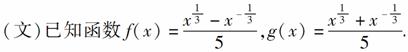
(1)证明 f ( x )是奇函数,并求其单调区间;
(2)分别计算 f (4)-5 f (2) g (2)和 f (9)-5 f (3) g (3)的值,并由此概括一个涉及函数 f ( x )、 g ( x )的对所有非零实数 x 都成立的等式,并证明.
简单的高一三角函数!求解,在线等!1、使不等式1+tanx大于等于0成立的集合是?2、若函数f(x 2020-04-27 …
二次函数a.b.c的大小分别决定与什么?C等于0或大于0或小于0AB等于0或大于或等于0函数分别是 2020-05-13 …
偶函数都要是偶数项吗?X^2+b x+3若是偶函数b要等于0因为是奇数项.那么3...偶函数都要是 2020-05-16 …
指数与对数函数1、函数Y=lg(2/1+x-1)的图像关于什么对称.2、函数y=a^x-2+3(a 2020-06-08 …
已知一个反比例函数和一个一次函数,当x=2时,它们的值分别为1和2,当X=4时,它们的值相等,求两 2020-06-27 …
已知函数fx=1g(3的x次方-3)求函数fx的定义域和值域.设函数h已知函数fx=1g(3的x次 2020-07-25 …
初等复合函数问题求函数y=(x+sin²X)³的导数.y′=[(x+sin²x)³]′=3(x+s 2020-08-02 …
高一函数的题目在线等急求1、已知函数f(x)=x-1/x+1,x随[1,3],求函数的最大值和最小值 2020-12-08 …
高一下反函数1.若函数f(x)=a^x+1的反函数为单调递减函数,则a的取值范围是2.函数f(x)= 2020-12-08 …
1两函数相等那么导数相等.2两导数相等则两函数相等.3函数越大导数越大.4导数越大函数越大.(这四句 2020-12-08 …