早教吧作业答案频道 -->数学-->
在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α(0°<α<360°)(Ⅰ)如图①,
题目详情
在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α(0°<α<360°)
(Ⅰ)如图①,当α=90°时,求AE′,BF′的长;
(Ⅱ)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
(Ⅲ)若直线AE′与直线BF′相交于点P,在旋转过程中当点P在坐标轴上时,分别表示出此时点E′、D′、F′的坐标(直接写出结果即可).
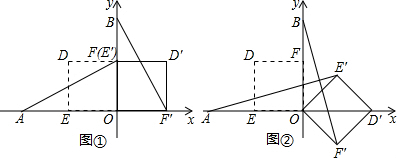
(Ⅰ)如图①,当α=90°时,求AE′,BF′的长;
(Ⅱ)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
(Ⅲ)若直线AE′与直线BF′相交于点P,在旋转过程中当点P在坐标轴上时,分别表示出此时点E′、D′、F′的坐标(直接写出结果即可).

▼优质解答
答案和解析
(1)当α=90°时,点E′与点F重合,如图①.
∵点A(-2,0)点B(0,2),
∴OA=OB=2,
∵点E,点F分别为OA,OB的中点,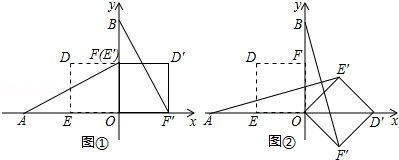
∴OE=OF=1,
∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的,
∴OE′=OE=1,OF′=OF=1.
在Rt△AE′O中,
AE′=
=
.
在Rt△BOF′中,
BF′=
=
.
∴AE′,BF′的长都等于
;
(2)当α=135°时,如图②.
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得,
∴∠AOE′=∠BOF′=135°.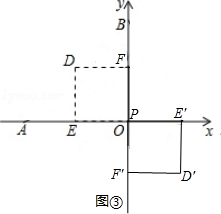
在△AOE′和△BOF′中,
,
∴△AOE′≌△BOF′(SAS).
∴AE′=BF′,且∠OAE′=∠OBF′.
∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB,∠CAO=∠CBP,
∴∠CPB=∠AOC=90°,
∴AE′⊥BF′;
(3)点E′(1,0)、D′(1,-1)、F′(0,-1)
如图③,直线AE′与直线BF′相交于点P,当点P在坐标轴上时,α=180°,P与O重合,
∵OE′=OF′=1,
∴点E′(1,0)、D′(1,-1)、F′(0,-1).
∵点A(-2,0)点B(0,2),
∴OA=OB=2,
∵点E,点F分别为OA,OB的中点,

∴OE=OF=1,
∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的,
∴OE′=OE=1,OF′=OF=1.
在Rt△AE′O中,
AE′=
| OA2+OE2 |
| 5 |
在Rt△BOF′中,
BF′=
| OB2+OF2 |
| 5 |
∴AE′,BF′的长都等于
| 5 |
(2)当α=135°时,如图②.
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得,
∴∠AOE′=∠BOF′=135°.

在△AOE′和△BOF′中,
|
∴△AOE′≌△BOF′(SAS).
∴AE′=BF′,且∠OAE′=∠OBF′.
∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB,∠CAO=∠CBP,
∴∠CPB=∠AOC=90°,
∴AE′⊥BF′;
(3)点E′(1,0)、D′(1,-1)、F′(0,-1)
如图③,直线AE′与直线BF′相交于点P,当点P在坐标轴上时,α=180°,P与O重合,
∵OE′=OF′=1,
∴点E′(1,0)、D′(1,-1)、F′(0,-1).
看了在平面直角坐标系中,O为原点,...的网友还看了以下:
如图所示是A-F六种物质之间相互转化关系图.已知B为紫红色固体单质,E为碱,F为蓝色絮状沉淀.(1 2020-04-11 …
(2013•百色)如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的 2020-05-16 …
高二数学 如图,F为椭圆x²/a²+y²/b²=1(a>b>0)的右焦点,点P在椭圆上,△POF是 2020-05-16 …
初二一道图形题如图,F为△的边BD上一点,过点B作BA平行EF,交DE的延长线于点A,过点DC平行 2020-06-27 …
已知函数f(x)=的图象为曲线C,函数g(x)=ax+b的图象为直线l.(1)当a=2,b=-3时 2020-07-20 …
如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC长为半 2020-07-20 …
如图所示金属导线框可以绕转轴OO′转动,当流过导线框的电流如图所示时,导线框受安培力合力F及导线框 2020-07-31 …
如图,在▱ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、 2020-11-01 …
12、如图,在长方形ABCD中,AB=2cm,AD=4cm,E、F分别为AD、BC的中点,分别以C, 2020-11-26 …
如图,F为平行四边形ABCD的边BC的延长线上的一点,且CF=BC,连接AF交CD于点E,对 2021-01-02 …