早教吧作业答案频道 -->数学-->
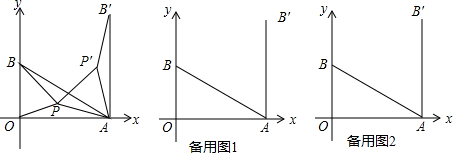
如图,在平面直角坐标系中A(3,0),B(0,1),点P为△OAB内任一点,连PO、PA、PB,将△ABP绕着点A顺时针旋转60°得到△AB′P′,连PP′.(1)求点B′的坐标;(2)当△OPA与△APB满足什么
题目详情
如图,在平面直角坐标系中A(
,0),B(0,1),点P为△OAB内任一点,连PO、PA、PB,将△ABP绕着点A顺时针旋转60°得到△AB′P′,连PP′.
(1)求点B′的坐标;
(2)当△OPA与△APB满足什么条件时,PO+PA+PB的值最小,并求出此最小值;
(3)试直接写出(2)中的点P坐标.
| 3 |
(1)求点B′的坐标;
(2)当△OPA与△APB满足什么条件时,PO+PA+PB的值最小,并求出此最小值;
(3)试直接写出(2)中的点P坐标.

▼优质解答
答案和解析
(1)∵A(
,0),B(0,1)
∴AB=2,∠BAO=30°
∵将△ABP绕着点A顺时针旋转60°得到△AB′P′
∴AB′=2,∠B′AO=90°
∴B′(
,2)
(2)由旋转可得,△APP′是等边三角形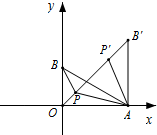
∴PP′=PA
又∵P′B′=PB
∴PO+PA+PB=PO+PP′+P′B′
∴如图,当O、P、P′、B′四点共线时,PO+PA+PB的值最小
∴当∠OPA=∠APB=∠AP′B′=120°时,PO+PA+PB的值最小
此时,PO+PA+PB=OB′=
=
(3)如图,将(2)中的△OPB绕着点O逆时针旋转60°得到△OB″P″,则∠BOB″=60°,OB″=OB=1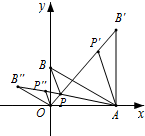
∴点B的坐标为(-
,
)
由(2)可知A、P、P″、B″四点共线
∴点P为OB′与AB″的交点
根据A、B″两点的坐标可得直线AB″的解析式为y=-
x+
根据B′的坐标可得直线OB′的解析式为y=
x
联立方程组,解得P(
,
| 3 |
∴AB=2,∠BAO=30°
∵将△ABP绕着点A顺时针旋转60°得到△AB′P′
∴AB′=2,∠B′AO=90°
∴B′(
| 3 |
(2)由旋转可得,△APP′是等边三角形

∴PP′=PA
又∵P′B′=PB
∴PO+PA+PB=PO+PP′+P′B′
∴如图,当O、P、P′、B′四点共线时,PO+PA+PB的值最小
∴当∠OPA=∠APB=∠AP′B′=120°时,PO+PA+PB的值最小
此时,PO+PA+PB=OB′=
22+(
|
| 7 |
(3)如图,将(2)中的△OPB绕着点O逆时针旋转60°得到△OB″P″,则∠BOB″=60°,OB″=OB=1

∴点B的坐标为(-
| ||
| 2 |
| 1 |
| 2 |
由(2)可知A、P、P″、B″四点共线
∴点P为OB′与AB″的交点
根据A、B″两点的坐标可得直线AB″的解析式为y=-
| ||
| 9 |
| 1 |
| 3 |
根据B′的坐标可得直线OB′的解析式为y=
2
| ||
| 3 |
联立方程组,解得P(
| ||
| 7 |
看了如图,在平面直角坐标系中A(3...的网友还看了以下:
1、设ABCD为自然数,且a^2+b^2=c^2+d^2,证:a+b+c+d为合数2、若在三角形中 2020-05-14 …
曲线C:y^2=x+1和定点A(3,1),B为曲线C上任意点.若AP向量=2倍的PB向量,当点B在 2020-05-16 …
正方形ABCD的边长为a,PA垂直于ABCD,且PA=a,求二面角A-PB-C,B-PC-D的大小 2020-05-16 …
.三角形PAB中,PA垂直PB,PA=a,PB=b三角形PAB中,PA垂直PB,PA=a,PB=b 2020-05-19 …
读下图,回答各题。小题1:若图示为热力环流形势,则a地与b地的气压(P)和气温(T)A.Pa>Pb 2020-06-13 …
1.已知点A(2,3),B(4,5)在x轴上是否存在点P使|PA-PB|的值最小,若存在,请求出点 2020-07-26 …
已知A(-√5,0),B(√5,0),动点C到A,B两点的距离之和为6.(1)求C的轨迹方程(2) 2020-07-31 …
已知点A在数轴上对应当数为a,点B对应的数为b(1)设点P在数轴上对应的数为x,当绝对值PA-绝对值 2020-12-07 …
20.若i是整型变量,pb是基本型为整型的指针变量,则正确的赋值表达式是()A.pb20.若i是整型 2020-12-31 …
计算机二级27.以下说明语句中,没有语法错误的是。A.inta,*pa=&a,*pb=*pa;B.i 2021-01-01 …