早教吧作业答案频道 -->数学-->
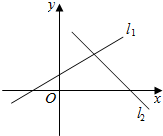
已知直线l1:ax-2y=2a-4与l2:2x+a2y=2a2+4.(1)求证:直线l1与l2都过同一个定点.(2)当0<a<2时,l1,l2与两坐标轴围成一个四边形,问:a取何值时,这个四边形的面积最小?求出这个最小
题目详情
已知直线l1:ax-2y=2a-4与l2:2x+a2y=2a2+4.
(1)求证:直线l1与l2都过同一个定点.
(2)当0<a<2时,l1,l2与两坐标轴围成一个四边形,问:a取何值时,这个四边形的面积最小?求出这个最小值.
(1)求证:直线l1与l2都过同一个定点.
(2)当0<a<2时,l1,l2与两坐标轴围成一个四边形,问:a取何值时,这个四边形的面积最小?求出这个最小值.
▼优质解答
答案和解析
 证明:(1)由l1:ax-2y-2a+4=0变形得:
证明:(1)由l1:ax-2y-2a+4=0变形得:
a(x-2)-2y+4=0,
所以,当x=2时,y=2,
即直l1过定点(2,2).
由l2:2x+a2y-2a2-4=0变形得a2(y-2)+2x-4=0,
所以当y=2时,x=2,
即直线l2过定点(2,2),
(2)如图示:
直线l1与y轴交点为A(0,2-a),直线l2与x轴交点为B(a2+2,0),如图:
由直线l1:ax-2y-2a+4=0知,直线l1也过定点C(2,2),
过C点作x轴垂线,垂足为D,于是:
S四边形AOBC=S梯形AODC+S△BCD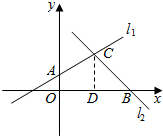
=
(2-a+2)•2+
a2•2
=a2-a+4,
∴当a=
时,S四边形AOBC最小.
故当a=
时,所围成的四边形面积最小值为:
.
 证明:(1)由l1:ax-2y-2a+4=0变形得:
证明:(1)由l1:ax-2y-2a+4=0变形得:a(x-2)-2y+4=0,
所以,当x=2时,y=2,
即直l1过定点(2,2).
由l2:2x+a2y-2a2-4=0变形得a2(y-2)+2x-4=0,
所以当y=2时,x=2,
即直线l2过定点(2,2),
(2)如图示:
直线l1与y轴交点为A(0,2-a),直线l2与x轴交点为B(a2+2,0),如图:
由直线l1:ax-2y-2a+4=0知,直线l1也过定点C(2,2),
过C点作x轴垂线,垂足为D,于是:
S四边形AOBC=S梯形AODC+S△BCD

=
| 1 |
| 2 |
| 1 |
| 2 |
=a2-a+4,
∴当a=
| 1 |
| 2 |
故当a=
| 1 |
| 2 |
| 15 |
| 4 |
看了已知直线l1:ax-2y=2a...的网友还看了以下:
求求个位了,1.已知两点在数轴上的距离为2008,且两点所表示的数互为相反数,则这两数分别是()2 2020-04-27 …
高一数学——直线与直线的方程1.已知两直线ax+by+1=0和mx+ny+1=0的交点为P(2,3 2020-05-16 …
1.已经两点A(1,1),B(3,6),动点C(X,Y),使三角形ABC的面积恒为3,求点C的轨迹 2020-05-22 …
1.已知两点A(-2,-2),B(2,2),求满足条件|PA|-|PB|=4的动点P的轨迹方程.我 2020-07-02 …
1.已知两个自然数的和是60,它们的最大公约数与最小公倍数之和是84,求这两个自然数各是多少?2. 2020-07-06 …
给出下列4个条件(1)已知两腰.给出下列4个条件:(1)已知两腰(2).已知底边和顶角(3)已知顶 2020-07-29 …
1.已知两点A(-1,-5),B(3,-2),直线L的倾斜角是直线AB的一半,求L的斜率2.直线L 2020-07-31 …
直线的点斜式方程1已知两点p(x1,y2),q(x1,y2),如果x1≠x2,那么直线pq的斜率k 2020-08-01 …
1.已知两条木条,一根长60cm,另一根长100cm,将它们的一端重合,放在同一条直线上,则两根木条 2020-12-28 …
可以从以下选一道或两道,三道更好,1.已知两点a(—1,3),b(5,3),若a关与点b的对称点为c 2021-01-10 …