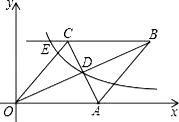
如图，已知：如图，在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y=kx（x>0）经过D点，交BC的延长线于E点，且OB•AC=160，有下列四

Question

如图，已知：如图，在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y= (k)/(x)（x>0）经过D点，交BC的延长线于E点，且OB•AC=160，有下列四个结论：
①双曲线的解析式为y= (40)/(x)（x>0）；
②E点的坐标是（5，8）；
③sin∠COA= (4)/(5)；
④AC+OB=12 √(5)．
其中正确的结论有___（填上序号）．

Answer 1

①过点C作CM⊥x轴于点M，如图1所示．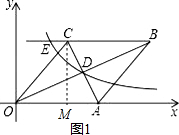
∵OB•AC=160，四边形OABC为菱形，
∴S_△OCA=(1)/(2)OA•CM=(1)/(4)OB•AC=40，
∵A点的坐标为（10，0），
∴CM=8，OM=√(OC2-CM2)=6，
∴点C（6，8），点B（16，8）．
∵点D为线段OB的中点，
∴点D（8，4），
∵双曲线y=(k)/(x)（x>0）经过D点，
∴k=8×4=32，
∴双曲线的解析式为y=(32)/(x)（x>0），
∴①不正确；
②∵点E在双曲线y=(32)/(x)（x>0）的图象上，且E点的纵坐标为8，
∴32÷8=4，
∴点E（4，8），
∴②不正确；
③∵sin∠COA=(CM)/(OC)=(4)/(5)，
∴③正确；
④在Rt△CMA中，CM=8，AM=OA-OM=10-6=4，
∴AC=√(CM2+AM2)=4√(5)，
∵OB•AC=160，
∴OB=8√(5)，
∴AC+OB=12√(5)．
∴④成立．
综上可知：③④成立．
故答案为：③④．