如图，点A、B、C在⊙O上，点B是AC的中点，∠ABC=∠AOC，将四边形AOCB绕点A按顺时针方向旋转一定角度后，点C落在圆上的点D处，连结OD．（1）求证：四边形AOCB为菱形；（2）若⊙O的半径为2，

Question

如图，点A、B、C在⊙O上，点B是

AC

的中点，∠ABC=∠AOC，将四边形AOCB绕点A按顺时针方向旋转一定角度后，点C落在圆上的点D处，连结OD．

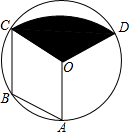
（1）求证：四边形AOCB为菱形；
（2）若⊙O的半径为2，求图中阴影部分的面积．

Answer 1

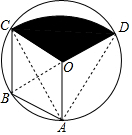证明：（1）连接OB，
∵点B是

AC

的中点，
∴∠COB=∠AOB=(1)/(2)∠AOC，
∵OA=OB=OC，
∴△AOB≌△COB（SAS），
∴∠CBO=∠ABO=(1)/(2)∠ABC，
∵∠ABC=∠AOC，
∴∠CBO=∠COB，
∴BC=OC，
∴AB=AO=OB=OC=BC，
∴四边形AOCB为菱形；

（2）连接AC、AD，
∵AC=AD，AO=AO，OC=OD，
∴△AOC≌△AOD（SSS），
∴∠CAO=∠DAO=(1)/(2)∠CAO，
∵AB=AO=OB=OC=BC，
∴△ABO和△CBO是等边三角形，
∴∠OCB=∠OAB=60°，
∵四边形AOCB是菱形，
∴AC⊥OB，∠OAC=∠OCA=30°，
∴∠CAD=2∠OAC=60°，
∵OA=2，∠OAC=30°
∴AC=2√(3)，
∴S_扇形CAD=(60π•(2√(3))2)/(360)=2π，
∴S_△AOC=(1)/(2)×1×2√(3)=√(3)，
∴S_阴影=S_扇形CAD-2S_△AOC=2π-2√(3)．